
Solución problema 37.
| Teorema
de Ceva. Sean a, b c, los vértices de un triángulo y tres puntos
a' de bc, b' de ca, y c' de ab sobre los lados de este triángulo. Entonces
las tres rectas aa', bb', y cc' son concurrentes si y sólo si se tiene:
a'b / a'c b'c / b'a c'a/ c'b = - 1 |
(En la tradición, llamaremos ABC los vértices)
Berger, M (1.990). Géomètrie.
Nathan. LUÇON
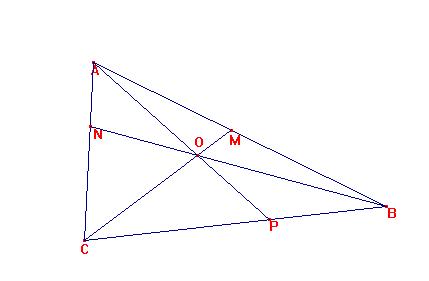
Sea ABC el triángulo y M,N, y P los tres puntos tales que
AP BN y CM se corten en un punto O interior al triángulo
(Demostremos así la necesidad de la relación).


Si trazamos el segmento paralelo a BA por P, tenemos:
Tenemos así los siguientes triángulos semejantes: OTP con OMA, y CPT con CBM.
tenemos las proporciones: PT/ PO = AM / AO, y CP/PT =CB/BM.
Luego, es, [1] CP/PO = (AM CB )/(AO BM).
De igual manera, tomando una paralela por P a CA, tendremos que:
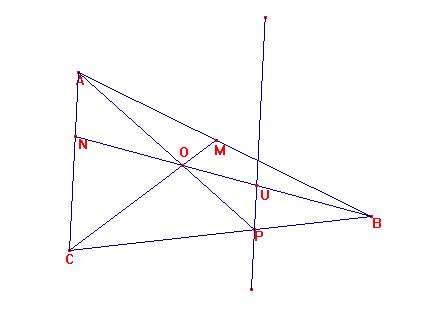
El triángulo OPU es semejante a OAN y el BPU al BCM.
Luego: PU/PO = AN/ AO, y BP/PU= BC/CN, de donde se tiene:
[2] BP/PO = (AN BC)/(AO CN)
Dividendo [1] entre [2], queda: (CP/PO) (PO/BP) = ((AM CB )/(AO BM))/( (AN BC)/(AO CN)).
Simnplificando, es: CP/BP = (AM CB AO CN)/ (AO BM AN BC).
Es decir, CP/BP = - (AM CN)/ ( BM AN),
y, c. q. d., es: (CP BM AN) / (BP AM CN) = -1
Veamos ahora la suficiencia.
Supongamos que se verifica que (CP BM AN) / (BP AM CN) = -1[3],
con P, M, y N sobre AB, AC y BC, respectivamente.
Si C M y BN se cortan sobre un punto S, , y unimos A con S, AS cortará a BC en un punto P'.
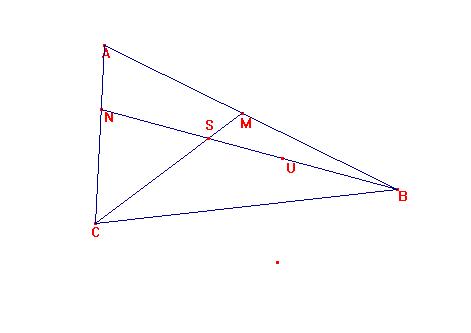
Por la condición necesaria, debe ser:
(CP' BM AN) / (BP' AM CN) =-1[4], y, dividendo [3] entre [4], queda:
(CP BM AN) (BP' AM CN)/ (BP AM CN) (CP' BM AN)= 1, es decir:
CP BP' / BP CP' =1, Es decir, CP / BP = CP' /BP', y por las propiedades de
las proporciones,
(CP + BP)/ BP = (CP' + BP')/BP', es decir, CB/BP = CB/ BP', luego, c.q.d,
es P=P'.
Ricardo Barroso (Con sugerencias de Marco de Lanuza (1.964): Matemátcas. Curso Prunivesitario)