Problema 37
| Teorema de Ceva. Sean a, b c, los vértices de un triángulo y tres puntos a' de bc, b' de ca, y c' de ab sobre los lados de este triángulo. Entonces las tres rectas aa', bb', y cc' son concurrentes si y sólo si se tiene: a'b / a'c b'c / b'a c'a/ c'b = - 1 |
Berger, M (1.990). Géomètrie. Nathan. LUÇON
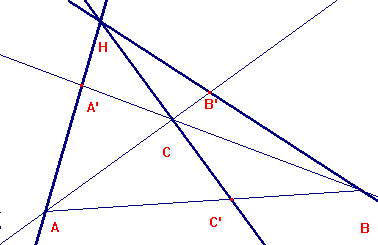
Teorema de Ceva en un triángulo obtusángulo con H exterior al triángulo. Veamos la necesidad.
Sea ABC, como tradicionalmente se denominan los vértices, obtuso en C, y sea H un punto exterior a ABC. Es:


Debemos analizar la relación: A'B/A'C B'C/B'A C'A/C'B.
Tracemos por C' una paralela al lado BC, que cortará a AH en T:
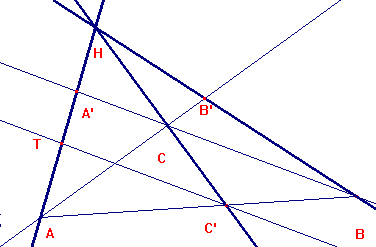
Tenemos las siguientes relaciones:
los triángulos AC'T y ABA' son semejantes, y también lo son los HC'T y HCA'.
Luego es : AC'/AB=C'T/BA', y HC/CA'=HC'/C'T, de donde se tiene, multiplcando, que:
[1] AC'/AB HC/CA' =HC'/BA'.
Si trazamos ahora una paralela a AC por C', tendremos el punto U de corte con la recta BH.
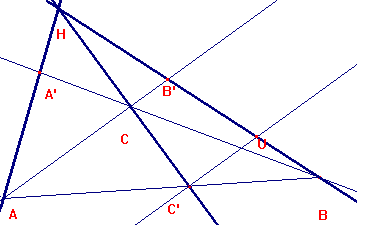
Los triángulos BC'U y BAB' son semejantes, y los HC'U y HCB' también lo son. Luego es:
BC'/BA=C'U/AB', y por otra parte, es: HC/CB'=HC'/C'U. Multiplicando es:
[2] BC'/BA HC/CB'= HC'/AB'.
Dividiendo [1] entre [2], es:
AC'/AB BA/BC' HC/CA' CB'/HC = HC'/BA' AB'/HC',
De donde: AC'/BC' CB'/CA' BA'/AB'=-1, y por ello, A'B/A'C B'C/B'A C'A/C'B = -1, CQD.
Veamos la suficiencia.
Si en un triángulo obtusángulo tenemos que
Supongamos que se verifica que (A'B B'C C'A) / (A'C B'A C'B) = -1[3]
con C', B', y A' sobre AB, AC y BC, respectivamente.
Si C C` y BB' se cortan sobre un punto S, y unimos A con S,
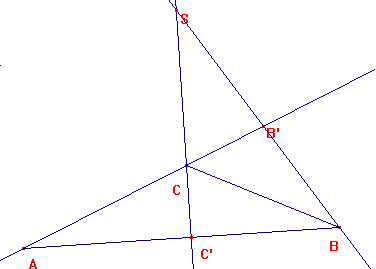
Por la condición necesaria debería ser:
XB/XC B'C/B'A C'A/C'B = -1 [4], Siendo X el punto de corte de BC con AS.
Dividiendo [3] entre [4], queda:
(A'B B'C C'A) / (A'C B'A C'B)/(XB/XC B'C/B'A C'A/C'B )= 1, es decir,
A'B XC /A'C XB =1, o bien, XB/XC = A'B/A'C, y, por las propidades de las proporciones,
(XB-XC)/XC = (A'B-A'C)/A'C, y BC/XC = BC/A'C, de donde se deduce que X=A', c.qd.
Ricardo Barroso.