Hablemos sobre un triángulo
Lo llamaremos ABC.
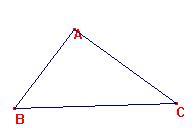
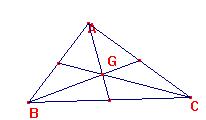
Las medianas convergen en un punto,
llamado baricentro, G
Para bisecar los ángulos
toma un ojo terrible.
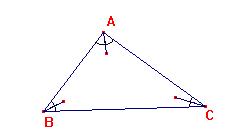
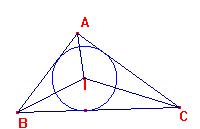
Pero tales bisectrices
se reunen en el incentro I
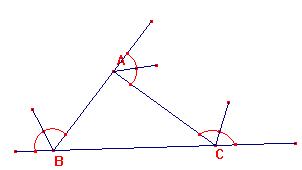
Hay tres bisectrices exteriores,
además de las otras
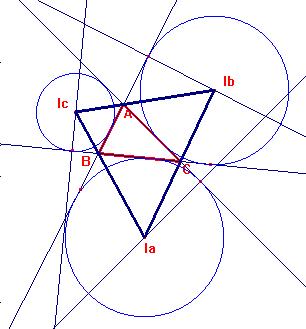
Se reunen en los excentros,
Ia Ib Ic
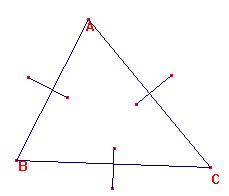
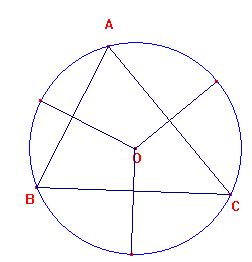
Las mediatrices
deben ir a través de los lados.
Todas radiando hacia fuera,
desde el circuncentro O
Aunque las alturas son tres,
señala mi hija Raquel,
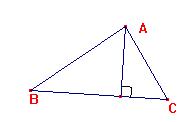
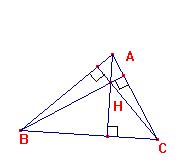
Hay un punto en todas ellas,
el ortocentro, H
Sus pies son a menudo llamados D, E y F
como en mi poesía
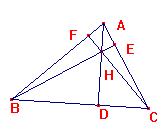
Y las medianas también tienen pies
que se les puede llamar A, B , C prima.
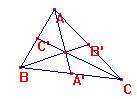
Estos pies (hay seis de ellos)
Pueden encontrarse también
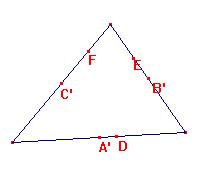
Alrededor de una circunferencia de nueve puntos
con centro N
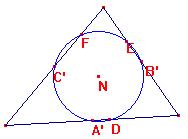
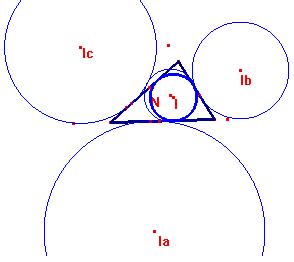
La circunferencia de los nueve puntos
Hace algo difícil
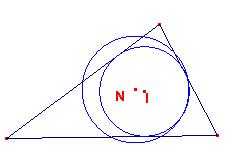
Toca la circunferencia inscrita
Y las tres exinscritas ¡También!
Los medial y órtico
Son triángulos inscritos
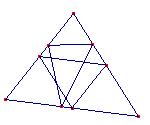
ABC-prima y DEF
Es como se describen
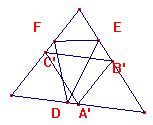
El medial tiene una figura
semejante a ABC
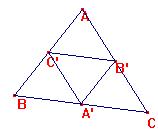
El órtico hace el menor camino
que toca los lados (todos)
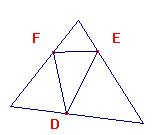
El medial tiene sus alturas
que se reunen en O
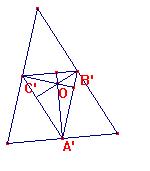
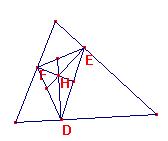
Las bisectrices del órtico
Pasan seguro por H
También los vértices de ambos están en la circunferencia de los nueve puntos
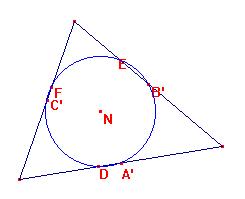
Sus mediatrices
se reunen en N seguro.
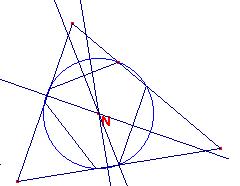
Tales triángulos tienen centros
la mayoría están alineados
Pero no de cualquier manera
Hay un orden asombroso

Cuatro centros están en la línea de Euler
Están relacionados en un orden estricto
Con N a medio camino entre O y H
Y G en la tercera parte.
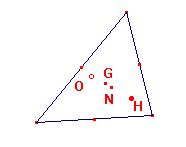
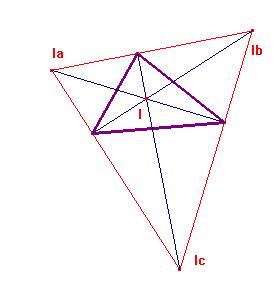
Otros cuatro se establecen
sobre un cuadrángulo ortocéntrico
El Incentro en el medio,
con los excentros alrededor
¿Quín pudiera pensar en un triángulo
Exactamente ABC
Que tuviera toda esa belleza escondida,
Para que pudiéramos encontrala y verla?