Sortais Y, R. (1997):  La géométrie du triangle. Hermann, editeurs des ciences et des arts ( Pág. 188)

Teorema de Feuerbach. Puntos de Feuerbach.

1ª parte Preliminar

Sea J una circunferencia de centro I y radio r.

Sea P un punto que no es de J.

Sea d una recta tangente a J que no contiene a P.

Sea P_J (P) la potencia de P respecto a J. Es: P_J (P)= IP ²- r ²

A todo punto M de d se le asocia el punto N de la recta PM tal que PM * PN= P_J (P).

Demostrar que cuando M describe d, N describe la circunferencia T, que contiene a P y es tangente a J.

Nociones utilizadas:

Concircularidad de cuatro puntos

Ángulos orientados de rectas

Potencia de un punto respecto a una circunferencia.

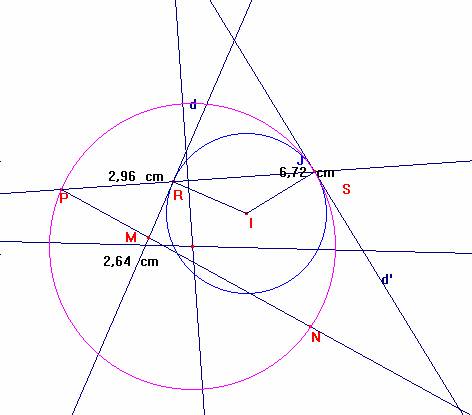
Sea R el punto de contacto de d y J.

La recta PR cortará a J en otro punto S distinto de R, ya que P no es de d.

Supongamos que M sea de d y que no sea R.

Sea d’ la recta tangente a J en S. Las rectas d y d’ son simétricas en relación a la mediatriz de RS.

Se tiene pues, que  (SR, d’) ≡ - (RS, d) (π)

Y (SP,d’) ≡ (RM,RS)  (π)                                          (1)

Por otra parte se tiene que: P_J (P)= PR * PS, y P_J (P) ≠ 0, porque P no es de J.

Como M ≠ R , entonces PM y PR son distintas, y por ello, N ≠ S

La condición  PM*PN=PR*PS es equivalente  a que los puntos M,N,R y S son concíclicos y diferentes de P, pues  P_J (P) ≠ 0 (2)

Además, la condición (2) significa que (RM, RS) ≡ (NP, NS ) (π)

Por otra parte, utilizando (1), la condición PM*PN = P_J (P) equivale a

(SP, d’) ≡ (NP, NS ) (π) (3)

De donde el conjunto de puntos N distintos de P y de S que verifican 3, es la circunferencia T que contiene a P y S, tangente a d’.

Supongamos que M es de d y M=R, entonces la relación PM*PN=PR*PS equivale a PN=PS, o sea, N=S.

Así, concluimos: Cuando M describe d, N describe T, tangente a J en S. La recta d’ es tangente común en S a J y T.