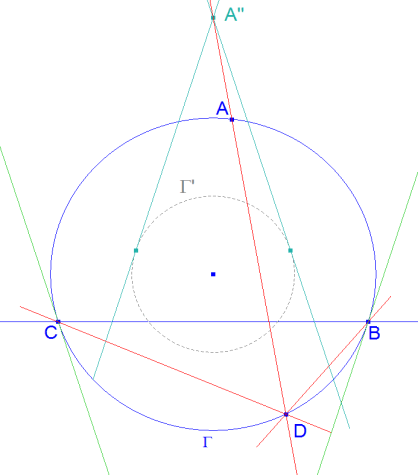
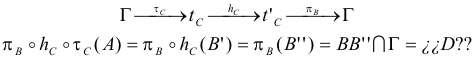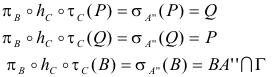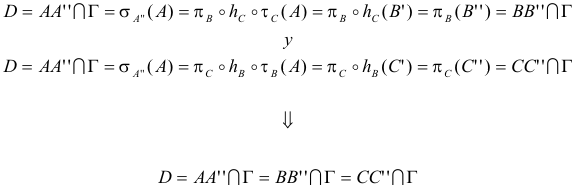Propuesto por François Rideau, Maître de Conférences à l'Université de Paris 7 102 Sea ABC un triángulo no equilátero. Sea Γ su circunferencia circunscrita y O su centro. Las tangentes en A, B , C a la misma forman un triángulo A' B' C'. Sea A'' B'' C'' el homotético de A'B'C' de centro O y razón -½. |
||
1._ |
Demostrar que ABC y A'' B'' C'' son homológicos*, cuyo centro D de homología está sobre Γ. |
|
*Homológicos en el sentido de Desargues: sus vértices dos a dos se encuentran sobre tres rectas que tienen un punto de concurrencia. |
||
2._ |
Demostrar que cada uno de los puntos A B C D puede ser obtenido a partir de los otros tres. (De la misma manera que D a partir de A B C) |
|
Rideau (2003): Le problème de Dobbs. Documento de trabajo. |
||
Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). |
||
|
||
INTRODUCCION |
||
|
||
|
Teorema
Una homografía del plano P → P' es una homología si y sólo si existe un punto D tal que, para todo P distinto de D, la recta PP' pasa por D.
Este punto D recibe el nombre de centro de la homología.
Puede verse la demostración en Sidler, Jean-Claude. Géométrie projective. Théorème 4.2. |
||
Por lo tanto, atendiendo al enunciado, debemos demostrar que:
|
||
|
||
|
El uso directo de homografías en el plano es algo engorroso, para buscar la imagen de un punto, deberíamos conocer previamente la imagen de cuatro puntos y luego hallar la imagen del punto deseado sabiendo que se conserva la razón doble de cuatro puntos alineados...
En el caso de que la homografía sea una homología, es más fácil gráficamente; pero eso es lo que tenemos que hallar en este problema.
Es mucho más sencillo, desde el punto de vista gráfico, trabajar con rectas proyectivas o con círculos y sus homografías, mucho más simples que las homografías planas.
Las ideas básicas de GEOMETRIA PROYECTIVA usadas en este problema pueden hallarse en el problema 137 de las páginas de RICARDO BARROSO CAMPOS
Para la demostración reinterpretaremos el enunciado y seguiremos el siguiente desarrollo: |
||
1._ |
Definiremos D como la imagen de A por una involución. |
|
2._ |
Definiremos B'' como la imagen de A por una composición de homografías y veremos que la proyección de B'' desde B coincide con D. |
|
3._ |
Definido el centro de homología, por medio de la involución, responderemos al apartado 2 del enunciado. |
|
|
||
DIBUJO DEL ENUNCIADO |
||
|
||
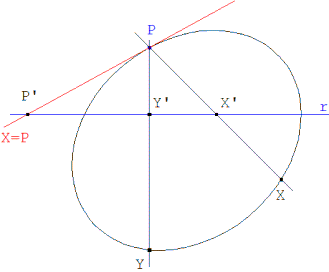
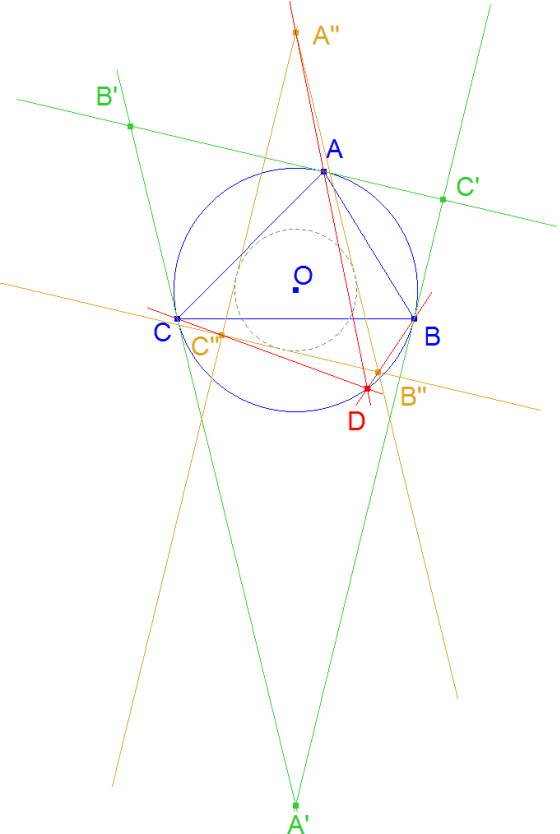 figura 1 figura 1
|
||
|
||
REINTERPRETACION DEL ENUNCIADO |
||
|
||
Sea un círculo Γ de centro en O. Sean dos puntos fijos B y C tal que B ∈ Γ y C ∈ Γ. Sea A un punto variable de Γ. Sean tB y tC las tangentes a Γ por B y C respectivamente. Sean t’B y t’C las imágenes de tB y tC por una homotecia de centro O y razón -½ … |
|
|
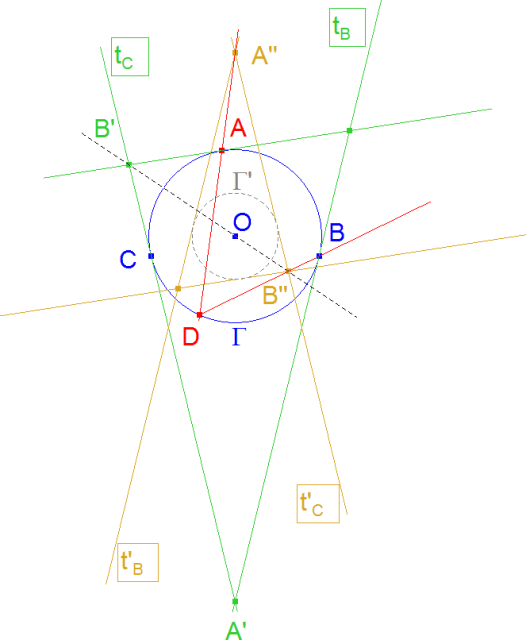 figura 2 figura 2
|
||
|
||
REDEFINICION DE BB''∩Γ Y CC''∩Γ |
||
|
||
t'C, imagen homotética de tC, es la tangente a Γ' paralela a tC y que deja a O entre t'C y tC. Γ' es la imagen de Γ por la homotecia de centro O y razón -½.
Vemos además que la tangente por A corta a tC en B' y B'' además de ser la imagen por la homotecia de centro O y razón -½, puede definirse por la siguiente homografía:
Si nos centramos en B' vemos que podemos definirlo con la siguiente homografía:
Otra homografía, definimos la proyección desde B de la recta t'C sobre el círculo Γ:
Como la composición de homografías es una homografía, podemos decir que pasamos desde un punto cualquiera A de Γ a otro punto D de Γ con la siguiente homografía.
( Si fuera D, el problema estaría resuelto )
DE MODO ANALOGO, PODEMOS CONSTRUIR CC''∩Γ. |
||
|
||
REDEFINICION DE AA''∩Γ |
||
|
||
Observando la figura, tB tC son fijos, pues también lo son Γ, B y C ; pero:
Observando la figura, t'B t'C son fijos, pues también lo son tB tC; pero:
Como A'' es un punto fijo, podemos definir la siguiente involución:
|
||
|
||
AHORA AA''∩Γ= BB''∩Γ = D |
||
|
||
Para que se cumpla el enunciado bastará probar que:
|
||
Teorema
Dos homografías entre rectas proyectivas que coinciden en tres puntos distintos son iguales.
Puede verse en Sidler, Jean-Claude. Géométrie projective. Corollaire 2.1. |
||
|
||
Sea P un punto de una cónica y sea r una recta que
no pasa por P. Sea X un punto de la cónica; la recta
PX corta a r en un punto X'. Es una biyección p, de
la cónica sobre la recta, llamada proyección de la
cónica sobre la recta r desde de un punto P.
Conserva la razón doble y su inversa es la proyección de la recta sobre la cónica desde un punto P.
Si X coincide con P, PX es la tangente a la cónica
en P. Sea h una homografía de la recta sobre sí misma y
h' una homografía de la cónica sobre sí misma:
Como
Puede verse en Sidler, Jean-Claude. Géométrie projective. 5.2.1. |
||
|
||
Vistos los dos recuadros anteriores podemos decir que :
|
||
Teorema
Homografías de un mismo círculo que coinciden en tres puntos distintos son iguales.
|
||
|
||
Comprobación del punto P (Primer punto de coincidencia)
|
||
|
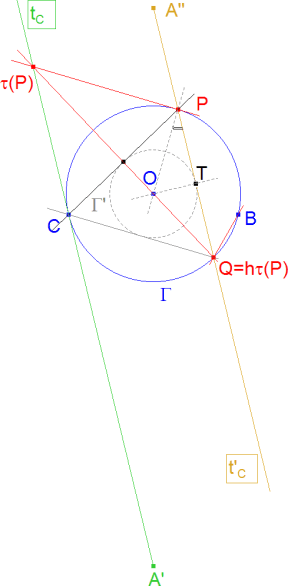
P es la intersección superior:
La tangente por P debe ser perpendicular a OP y si observamos la figura 4,
de lo que se deduce: ._ ΔPτ(P)C es equilátero ._ ΔPCQ es equilátero. Ahora bien Oτ(P) es bisectriz de ∠Pτ(P)C y por tanto también es bisectriz de ∠PQC, deducimos entonces:
Por otra parte:
|
|
De lo anterior deducimos el siguiente resultado:
|
||
|
||
Comprobación del punto Q (Segundo punto de coincidencia)
|
||
|
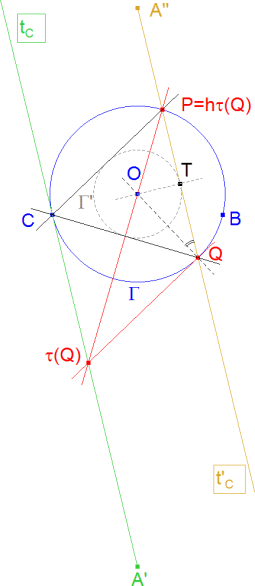
Q es la intersección inferior:
La tangente por Q debe ser perpendicular a OQ y si observamos la figura 5,
de lo que se deduce: ._ ΔQτ(Q)C es equilátero ._ ΔQCP es equilátero. Ahora bien Oτ(Q) es bisectriz de ∠Qτ(Q)C y por tanto también es bisectriz de ∠QCP, deducimos entonces:
Por otra parte:
|
|
De lo anterior deducimos el siguiente resultado:
resultado previsible si la homografía debe ser una involución. |
||
|
||
Comprobación del punto B (Tercer punto de coincidencia)
|
||
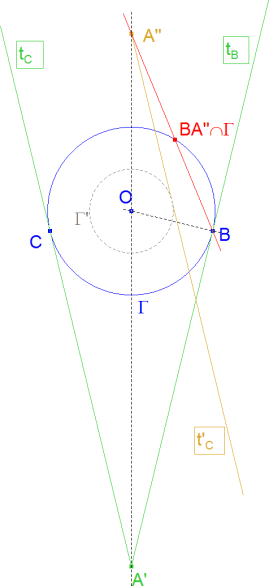 figura 6 figura 6
|
B es el punto dado en el enunciado. En este punto B, todo es más sencillo. La tangente por B no es otra que tB y si observamos la figura 6,
Pero además también
Y por último
También por definición
|
|
De lo anterior deducimos el siguiente resultado:
|
||
|
||
SOLUCION DEL APARTADO 1 DEL ENUNCIADO |
||
|
||
a._ |
|
|
b._ |
La coincidencia de las dos homografías en tres puntos distintos las hace idénticas:
|
|
c._ |
Por procedimiento análogo y considerando el punto C:
|
|
d._ |
Podemos pues escribir:
|
|
|
||
De (d) deducimos que los triángulos ΔABC y ΔA'' B'' C'' son homológicos, con centro de homología en D∈Γ.
c.q.d
PODEMOS DECIR QUE FIJADOS ABC, LA INVOLUCION σA'' DEFINE EL CENTRO DE HOMOLOGIA D. |
||
|
||
|
||
SOLUCION DEL APARTADO 2 DEL ENUNCIADO |
||
|
||
|
||
Supongamos, sin pérdida de generalidad, que tenemos BCD. Las tangentes en C y en B son las mismas que en el apartado anterior y su intersección es A' (sería ahora D') y A'' sería el mismo que en el caso anterior (sería ahora D''). Se cumplirá entonces que dados BCD:
Resultado previsible por ser una involución.
|
||
Pero hemos demostrado que la imagen de esta involución es el centro de la homología, entonces A es el centro de homología para los puntos BCD.
c.q.d. |
||
Análogamente para ACD y ABD definiremos el mismo tipo de involución. |
||