CITA EN EL DESIERTO

En el desierto del Sahara, y en tres puntos A, B y C, que forman los vértices de un triángulo equilátero de 700 km de lado, se encuentran tres vehículos cuyas velocidades respectivas son 20, 40 y 60 km/h. comunicados por radio con el centro de operaciones, reciben la orden de partir a reunirse lo antes posible.

¿Dónde está situado en el dibujo el punto de reunión?

 

SOLUCIÓN: Carmen Arriero Villacorta, profesora de Matemáticas del IES Ramón y Cajal de Madrid, y asesora de Nuevas Tecnologías de la Informacaión y Comunicación en el Centro de Apoyo al Profesorado de Hortaleza-Barajas de la Comunidad de Madrid (7 de julio de 2003).

A partir de los datos del problema se tiene:

 

Velocidad

Espacio recorrido

Vehículo que sale de A

20 km/h

x   km

Vehículo que sale de B

40 km/h

2x km

Vehículo que sale de C

60 km/h

3x km

 

Luego el punto de encuentro tiene que estar a una distancia de B y de C el doble y el triple respectivamente que de A.

 

 

Realizando el problema de forma experimental con Cabri se llegan a las siguientes conclusiones:

 

·                que la distancia del punto de encuentro al vértice A, es decir x, tiene que ser mayor que  del lado del triángulo pues si fuera menor los vehículos que salen de A y B no se encontrarían.

.

·                El punto de encuentro tiene que estar fuera del triángulo equilátero ya que el recorrido del vehículo que sale de C es mayor que el lado.

 

 A continuación se muestra una solución aproximada obtenida con Cabri a partir de las observaciones realizadas anteriormente.

 

 

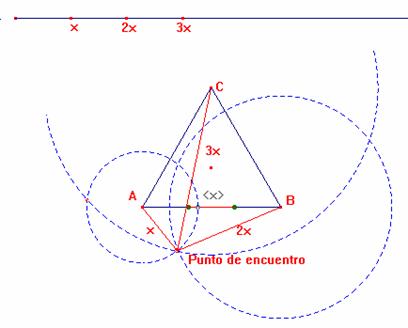
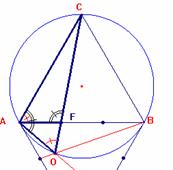
El punto de encuentro solución del problema se puede localizar de la siguiente forma:

 

1.      Dibuja el triángulo D ABC’ simétrico a D ABC respecto del lado AB y divide cada lado en tres partes iguales

2.      El punto O, intersección de los segmentos AD y BE, es el Punto de encuentro. Es decir, AO = 2 BO = 3 CO. Compruébalo con Cabri.

 

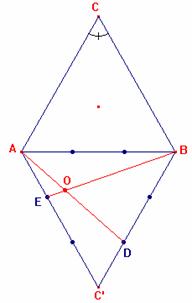
Demostración

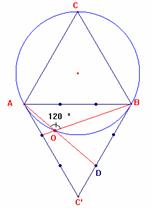
·                En el triángulo DAOB se cumple: РOAB + Ð ABO = 60º por construcción. De lo que se deduce que РAOB = 120º.

·                Observa que en el cuadrilátero AOBC los ángulos opuestos son suplementarios, por tanto el cuadrilátero es inscriptible en una circunferencia que coincide con la circunferencia circunscrita al triángulo.

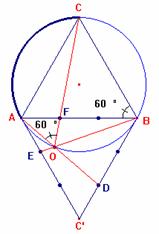
·                Al trazar el segmento CO, los ángulos РAOC y РABC abarcan el mismo arco por lo que РAOC = 60º.

·                También abarcan el mismo arco los ángulos ÐACO y ÐABO y como BE (prolongación de BO) corta al lado AC’ dividiéndolo en dos partes una doble que la otra, también el segmento CO corta al lado AB en el punto F, dividiéndolo en dos partes una doble que la otra, FB=2AF.

·                En el triángulo DAOB, por ser РAOC = 60º,  OF es la bisectriz del ángulo Ð AOB. Esto implica que los segmentos AF y FB (partes en que queda dividido el lado AB por la bisectriz OF) son proporcionales respectivamente a los lados AO y OB. Es decir,

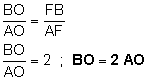
·                Comparando los ángulos de los triángulos D AOC y D AFC se llega a la conclusión de que son semejantes, por tanto sus lados tienen que ser proporcionales, cumpliéndose las siguientes igualdades

          Sustituyendo el valor del lado de DABC se obtiene

         

          De donde CO = 3 AO