Problema 109

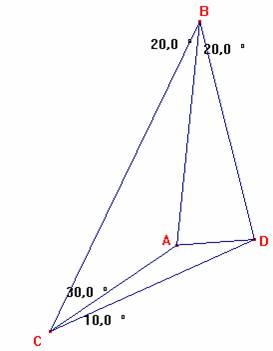
En la figura: Es el triángulo BCD, con A en el interior tal que:

< CBA = < ABD = 20º, < BCA = 30º, < DCA =10º.

Calcular < BDA, y demostrar que AB=BD.

Propuesto por Juan Carlos Salazar, Profesor de Geometría del Equipo Olímpico de Venezuela.

(Puerto Ordaz)

Salazar, J.C. (2003): Comunicación personal.

Solución de F. Damián Aranda Ballesteros profesor de Matemáticas del IES Blas Infante en Córdoba (5 de julio de 2003)

Como quiera que en el punto A concurren las cevianas CA, DA y BA se tendrá, por el Teorema de Menelao, la siguiente relación:

; donde x =<BDA

Despejando:

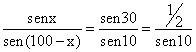.         En definitiva:

sen (100-x) = 2×senx×sen10  (1)

Observamos que, en efecto, para x=80 se verifica (1).

Veamos que para otro valor x¹80 no se verifica la anterior ecuación.

Sea  x= 80+a,  y sustituyamos este valor en (1). De este modo, obtenemos:

sen (20-a) = 2×sen(80+a)×sen10

sen20×cosa - cos20×sena = 2×(sen80×cosa + cos80×sena)×sen10 = 2 sen10 cos10 cosa + 2 sen10 sen10 sena

cos20×sena + 2 sen10 sen10 sena = 0

(cos²10 - sen²10 +2×sen²10 )×sena=0;            (cos²10 + sen²10)×sena = 0;                sena=0  Þ      a=0

En definitiva, el ángulo x=80 y así el triángulo BAD es isósceles, siendo AB=BD, c.q.d.

Saludos de F. Damián Aranda Ballesteros.