SOLUCIÓN PROBLEMA 61

PROFESOR: ARBEY LUQUE DÍAZ

INEM “José Eustasio Rivera” – Leticia – Amazonas (Colombia)

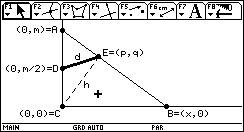
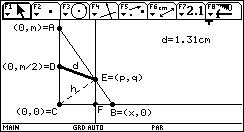
Se trata de demostrar que en la figura anterior, siendo m constante, x variable y h la altura triángulo ABC, la longitud del segmento d es constante.

PROCEDIMIENTO:

Se traza una perpendicular al eje X que pase por el punto E. Al punto de intersección entre dicha recta y el eje X se le etiqueta con la letra F.

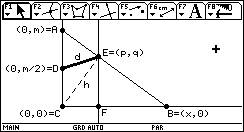
Es fácil ver que:

a) Los triángulos ACE y CEF son rectángulos en E y F, respectivamente.

b) Los ángulos ACE y CEF son congruentes, por ser alternos internos entre paralelas.

c) Los ángulos CAE y ECF son congruentes por ser complementarios de ACE y CEF, respectivamente.

d) Los triángulos ACE y CEF son semejantes, por a), b) y c).

e) Las relaciones y son verdaderas, por a) y d), respectivamente.

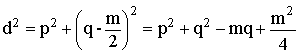Ahora, combinando las ecuaciones escritas en e) se obtiene que [1], y como d es la distancia entre los puntos D y E, resulta que [2].

Finalmente, combinando [1] y [2] se obtiene .

L.Q.Q.D.

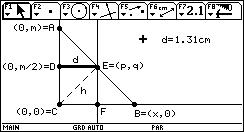
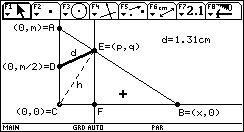
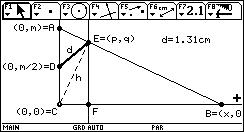
Midiendo la distancia entre los puntos D y E y moviendo el punto B, se comprueba lo demostrado.