Problema 61.-

Sea ACB un triángulo rectángulo en C con el cateto b constante.

Sea M el punto medio de AC, y D el pie de la altura del vértice C sobre la hipotenusa.

Demostrar que al variar el vértice B, DM permanece constante.

Solución de F. Damián Aranda Ballesteros

profesor de Matemáticas del IES Blas Infante en Córdoba

Sol:

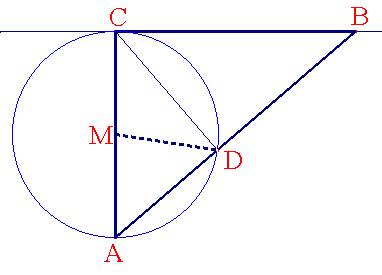El punto D, pie de la altura del vértice C sobre la hipotenusa, pertenece al arco capaz de 90º construido sobre el segmento AC y, por tanto, el segmento MD no es otra cosa que el radio de dicha circunferencia.

Por tanto MD = AC/2 = b/2 =cte.