DADO UN TRIÁNGULO ABC CUALQUIERA SE FIJA UN PUNTO X. DEMOSTRAR QUE CXB/AXC=c/d.

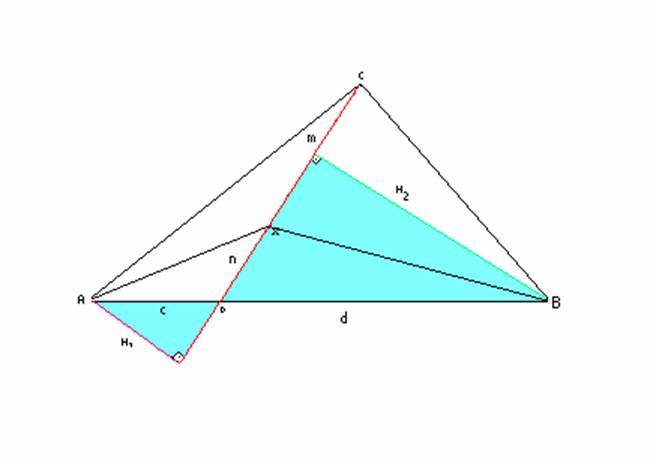
Queremos demostrar que:

que es lo mismo que:

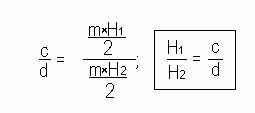
De donde vemos que la igualdad del enunciado se cunple si se cumple la última igualdad propuesta.

La X nos determina un ángulo alfa respecto a AB. Si se traza la tangente a CD, que pasa por X, tendremos un triángulo rectángulo cuya hipotenusa será D y H2 será su cateto mayor. Sus ángulos serán alfa, noventa menos alfa y noventa.

Se relacionan H2 y d por el teorema del seno y resulta que H2= d* sen α.

Como dicho triángulo es rectángulo, tenemos que

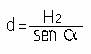
De igual modo si lo hacemos con el triángulo rectángulo cuya hipotenusa es c y su cateto mayor H1, obtenemos

Si despejamos el seno tenemos

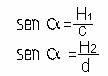
de donde se obtiene que:

Y QUEDA DEMOSTRADO

Maite y Alicia Peña Alcaraz, Alumnas del Colegio Porta Celi de Sevilla