Problema: Dado un triángulo ABC y un punto X, tal que AX corte a BC en un punto D, demuestra que el cociente entre los triángulos AXB y AXC es igual que el cociente BD entre BC:

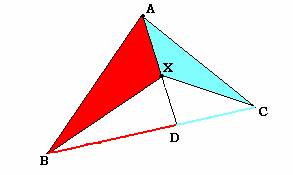
Lo primero que hemos hecho nosotras es demostrar una propiedad que luego hemos utilizado para resolver el problema.

Propiedad: Dado cualquier triángulo ABC y un punto cualquiera D sobre cualquiera de sus bases, entonces:

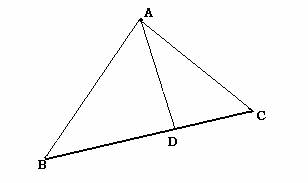
El área del triángulo ABD entre el área del triángulo ADC es igual que BD entre DC, ya que:

ABD= (BD * h_A) /2

ACD= (DC * h_B )/2

Y entonces al dividir el primero entre el segundo, te da BD/DC.

Una vez probado esto, si nos fijamos en el triángulo ABD del enunciado, vemos que:

ABX / BDX = AX / DX

Si nos fijamos ahora en el triángulo ACD, conseguimos:

ACX / CDX = AX / DX

De lo que se obtiene:

ABX / ACX = BDX / CDX

Y si ahora nos fijamos en el triángulo XBC, obtenemos que:

BDX / CDX = BD / DC

Luego:

ABX / ACX = BDX / CDX = BD / DC

Y de aquí:

ABX / ACX = BD / DC

Que es lo que se pretende demostrar.

Maite y Alicia Peña Alcaraz. Estudiantes de Primero de Bachillerato. Colegio Portaceli. Sevilla