Problema 68.-

Dado un triángulo ABC,

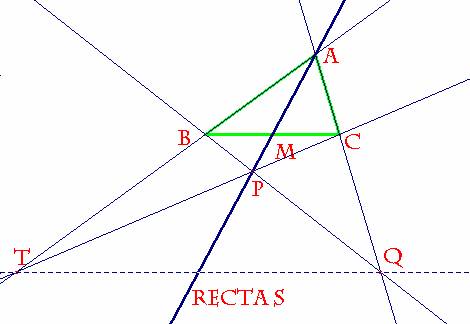
a)Tracemos la recta s que contiene a la mediana AM. Tomemos P, un punto cualquiera de s.

Tracemos las rectas BP, y CP, que cortarán a AC y a AB, o sus prolongaciones, en Q y T. Demostrar que TQ es paralela a BC.

Sol:

Apliquemos el Teorema de Ceva al triángulo ABC dado, ya que las tres cevianas construidas concurren en el punto P.

Esto significa que:

(1), pero como la recta s es la mediana correspondiente al vértice A, el punto M será el punto medio del lado BC. Así será MB=MC, y la expresión (1) adoptará la forma:

(2) es decir, existe una proporción entre los dos pares de lados que forman el mismo ángulo A

Por tanto, los triángulos ABC y ATQ serán ambos semejantes y el lado TQ será homólogo al lado BC por la homotecia de centro A y razón k. De este modo queda probado que TQ es paralela a BC.

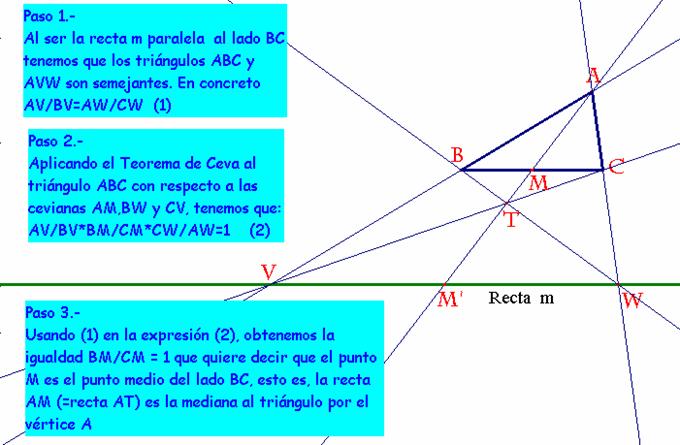
b) Sea la recta m es paralela a BC cortando a AB o su prolongación en V, y a AC o su prolongación en W.

Construyamos las rectas BW y CV, que se cortarán en T.

Demostrar que la recta AT contiene a la mediana al triángulo por el vértice A.

F. Damián Aranda Ballesteros, profesor de Matemáticas del IES Blas Infante en Córdoba