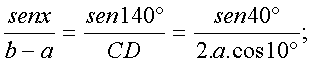Problema 69.-

Se tiene un triángulo isósceles ABC con ABC =100º.
Se construye D en la semirrecta de origen B que contiene a A tal que CA=BD. Calcular el ángulo ACD.

Construcción del triángulo inicial, donde CA = BD = b

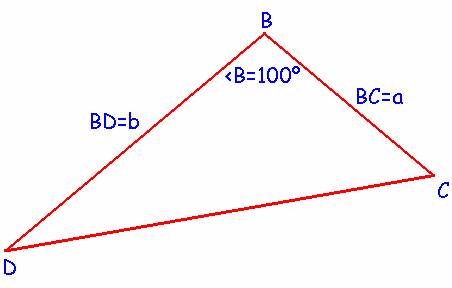
Consideramos ahora el triángulo DBC siguiente:

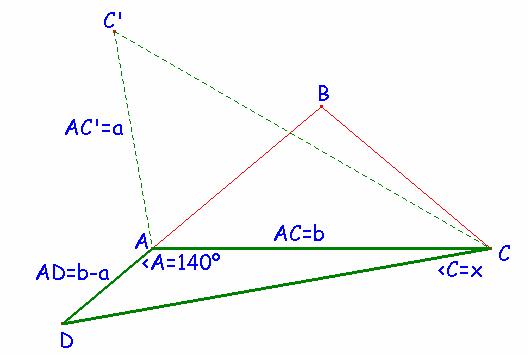
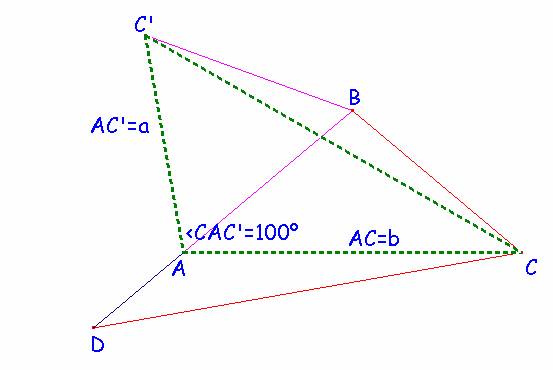
Como quiera que construyendo el triángulo equilátero exterior de base el lado AB = a, obtenemos el triángulo CAC’ equivalente al anterior DBC, pues tiene dos lados iguales así como el ángulo que forman.
Esto es así ya que:
AC= b , AC’= a y el ángulo comprendido entre ellos es igual a 40º+60º = 100º.

Luego entonces CC’ = CD y así el triángulo CBC’ es también isósceles de lados iguales BC = BC’ = a, y con ángulos en la base iguales a 10º ya que el ángulo en B sería igual a 100º+60º =160º.

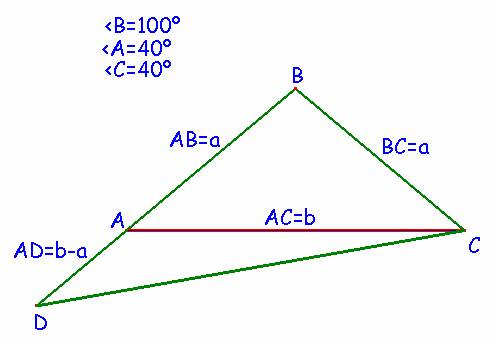
Por tanto, aplicando el teorema de los senos en este triángulo obtenemos que:

; ;

En definitiva: CD=2.a.cos10º

Con esta expresión de la medida del lado CD nos vamos a ir al triángulo ACD, volviendo a aplicar otra vez el teorema de los senos:

2.sen x .cos 10º = (b-a)/a .sen 40º = (b/a – 1). sen 40º;

Ahora bien, según el primer triángulo ABC, cos 40º = b /2×a Luego:

2.sen x .cos 10º = (2.cos 40º – 1). sen 40º = sen 80º – sen 40º.

Teniendo en cuenta que:

sen 80º – sen 40º = 2. cos 60º sen 20º = 2. ½ .2. sen 10º. cos 10º

entonces resultará que:

2.sen x .cos 10º = 2. sen 10º. cos 10º

de donde de deducimos que:

sen x = sen 10º y, como el ángulo en A es obtuso, no queda más remedio que ser x = 10º . (!!)

Solución de F. Damián Aranda Ballesteros profesor de Matemáticas del IES Blas Infante en Córdoba
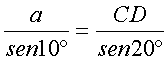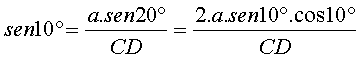