Problema 69.

Se tiene un triángulo isósceles ABC con ABC=100º.

Se construye D en la semirecta de origen B que contiene a A tal que CA=BD.

Calcular el ángulo ACD.

Solución de Damián Aranda Ballesteros (IES de Blas Infantes de Córdoba) / Ricardo Barroso Campos(Departamento de Didáctica de las Matemáticas, Universidad de Sevilla).

Sea ABC y construyamos el simétrico según la recta AB:

El triángulo CBE es tal que por construcción es isósceles en B (BE=BC), luego CBE=360º-100º-100º=160º, y BEC=BCE=10º.

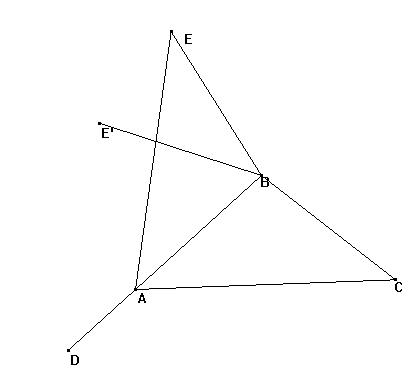
Tomemos ahora el simétrico BE' del segmento BE respecto a la recta BC:

El triángulo E'BC por ser simétrico del EBC, es tal que: BC=BE'=BA, y CBE'=160º.

Al ser el ánglo ABC=100º por construcción, es E'BA= E'BC-ABC=160º-100º=60º.

Así pues, E'BA es isósceles con un ángulo de 60º, y por ello, equilátero.

Consideremos el triángulo E'AC.

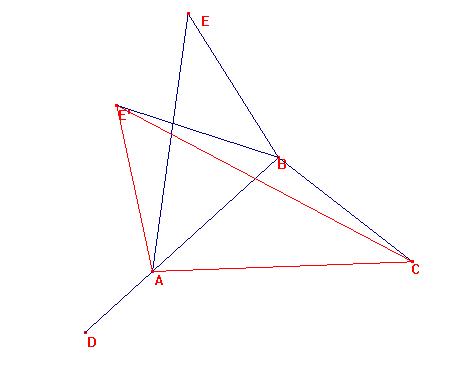
El ángulo E'AC= E'AB+BAC=60º+40º=100º.

Los triángulos E'AC y CBD tienen:

los ángulos E'AC=CBD=100º , los lados: E'A=E`B=EB=CB, y AC=BD.

Luego por el criterio de congruencia de triángulos, es CE'=DC.

Es decir, CE=CE'=DC. De igual manera, será DE=DC. ASí, pues, el triángulo

DCE es equilátero, y

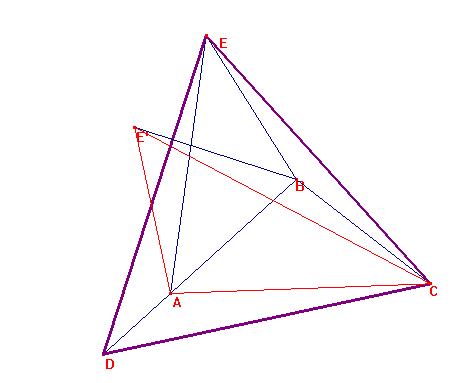
Por ello, DCA= 60º-BCA-BCE=60º-40º-10º=10º, como deseábamos obtener.