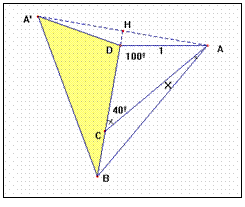
 Construyamos el triángulo ADB según las condiciones del problema, y obtengamos
el simétrico BDA’ respecto el lado DB. Podemos considerar un nuevo triángulo
de vértices ABA’
Construyamos el triángulo ADB según las condiciones del problema, y obtengamos
el simétrico BDA’ respecto el lado DB. Podemos considerar un nuevo triángulo
de vértices ABA’
No supone ninguna restricción suponer el lado AD = 1.
En tal caso el lado AC = DB = 2sen 50º, pues
aplicando el teorema del seno en el triángulo ADC tenemos ![]() de donde
de donde
![]()
Si consideramos el triángulo ADA’ El ángulo D es igual a 160º y cada uno de los otros dos ángulos vale 10º.
Aplicando nuevamente el teorema del seno en dicho triángulo obtenemos
![]() y de aquí
y de aquí
![]() .
.
Además es inmediato que DH ( que es la altura del triángulo ADA’) vale sen10.
El segmento BH es por construcción la altura del triángulo ABA’, y su valor es BD + DH = 2 sen50 + sen10.
Utilizamos el teorema de Pitágora para hallar
el lado AB. ![]()
![]()
![]()
![]()
![]()
y por tanto AB = BA’ = 2cos10 =AA’, lo que significa que el triángulo ABA’ es equilátero y sus ángulos miden 60º sexag. Â= 60º =X + 40º + 10º y de aquí X = 10º