Problema:

72.- Alineaciones

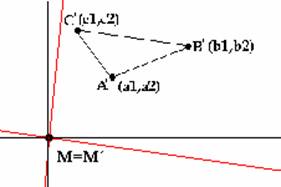
Sea ABC un triángulo en el plano afín euclideo P. Sea M un punto cualquiera del plano. Suponemos que: - la perpendicular por M a la recta AM corta a la recta BC en A' - la perpendicular por M a la recta BM corta a la recta CA en B' - la perpendicular por M a la recta CM corta a la recta AB en C' Demostrar que los puntos A', B' C' están alineados.

F.G.M. (Frère Gabriel-Marie)(1922): Cours de Géomètrie. Editions Mame.

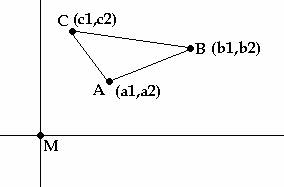
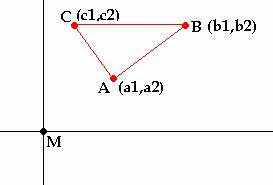
Si consideramos este triángulo en los ejes cartesianos, e intentamos ver que relaciones cumplen los puntos:

Las rectas AB (c), AC (b) y BC (a) serán:

a= (c2-b2)X -(c1-b1)Y +b2(c1-b1) -b1(c2-b2) =0

b= (c2-a2)X -(c1-a1)Y +a2(c1-a1) -a1(c2-a2) =0

c= (b2-a2)X -(b1-a1)Y +c2(b1-a1) -c1(b2-a2) =0

Las rectas desde M hasta cada punto son fáciles, tendrán de vector director el punto A, B o C, y de punto el (0,0), luego las perpendiculares por m serán las rectas:

A: a1X +a2Y =0

B: b1X +b2Y =0

C: c1X +c2Y =0

Luego los puntos A´, B´ y C´ serán la intersección de las rectas a, b, c con A, B y C, las perpendiculares por M:

C´:          X= (c2 ( a1 (b1-a1) – a2 (b2-a2) ) ) / ( c1 (b1-a1) +c2 (b2-a2) )

                Y= -(c1 ( a1 (b1-a1) – a2 (b2-a2) ) ) / ( c1 (b1-a1) +c2 (b2-a2) )

B´:           X= (b2 ( a1 (c1-a1) – a2 (c2-a2) ) ) / ( b1 (c1-a1) +b2 (c2-a2) )

                Y= -(b1 ( a1 (c1-a1) – a2 (c2-a2) ) ) / ( b1 (c1-a1) +b2 (c2-a2) )

A´:           X= (a2 ( b1 (c1-b1) – b2 (c2-b2) ) ) / ( a1 (c1-b1) +a2 (c2-b2) )

                Y= -(a1 ( b1 (c1-b1) – b2 (c2-b2) ) ) / ( a1 (c1-b1) +a2 (c2-b2) )

Y la condición indispensable para que los tres puntos estén alineados es que

(X_B – x_A) / (X_A-X_C) = (Y_B – Y_A) / (Y_A – Y_C)

Y si se efectúa la división se ve que es cierto siempre que se pueda poner b2=c2, lo cual es evidente que lo podemos hacer, basta con girar la figura del principio los ejes desde el origen para conseguir ésto: