Solución Saturnino Campo Ruiz, profesor de Matemáticas del I.E.S. Fray Luis de León (Salamanca)
Problema 72.- Alineaciones
Sea ABC un triángulo en el plano afín euclídeo P. Sea M un punto cualquiera del plano.
Suponemos que:
- la perpendicular por M a la recta AM corta a la recta BC en A'.
- la perpendicular por M a la recta BM corta a la recta CA en B'.
- la perpendicular por M a la recta CM corta a la recta AB en C '.
Demostrar que los puntos A', B' C ' están alineados.
Solución.-
 Nuestra solución se basa en la demostración de una propiedad para las
seis rectas de un haz, que sólo depende de la posición que mantienen entre
sí dichas rectas, y que, por tanto, se conserva al realizar proyecciones o
secciones.
Nuestra solución se basa en la demostración de una propiedad para las
seis rectas de un haz, que sólo depende de la posición que mantienen entre
sí dichas rectas, y que, por tanto, se conserva al realizar proyecciones o
secciones.
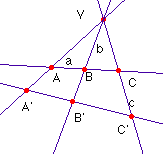
En la figura adjunta para las rectas a, b y c
concurrentes en V, y cortadas por una secante que determina los puntos
ABC, aplicando el teorema de los senos podemos escribir: ![]() y también
y también
![]() .
.
Dividiéndolas entre sí encontramos ![]() .
.
Es evidente que para la razón formada por sus proyecciones
en otra recta no paralela se obtiene una razón diferente ![]() , por eso
es más importante la razón doble que la simple, ya que esta última es invariante
por proyecciones y secciones.
, por eso
es más importante la razón doble que la simple, ya que esta última es invariante
por proyecciones y secciones.
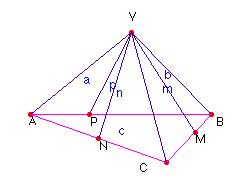 Si ahora disponemos de un triángulo ABC y otros tres
puntos M, N y P, cada uno alineado con dos vértices y otro punto
V no alineado con ninguna terna, como se indica en la figura, se tendrá
procediendo como antes:
Si ahora disponemos de un triángulo ABC y otros tres
puntos M, N y P, cada uno alineado con dos vértices y otro punto
V no alineado con ninguna terna, como se indica en la figura, se tendrá
procediendo como antes:
![]() . Tomamos
otra razón simple con los puntos M, B y C. Se tendrá:
. Tomamos
otra razón simple con los puntos M, B y C. Se tendrá:
![]() , y para
la determinada por N, C y A
, y para
la determinada por N, C y A ![]() . Multiplicándolas
entre sí, se eliminan las razones de las distancias al punto V, obteniendo
así un invariante proyectivo para las rectas del haz que concurren en V.
. Multiplicándolas
entre sí, se eliminan las razones de las distancias al punto V, obteniendo
así un invariante proyectivo para las rectas del haz que concurren en V.
![]() .
.
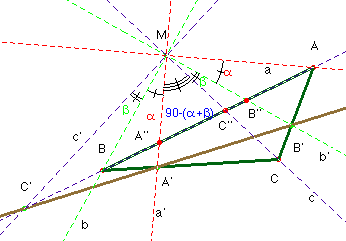 Para demostrar que los puntos A’, B’ C’ están alineados, vamos
a aplicar el teorema de Menelao al triángulo ABC. Es decir ver si vale
+1 el siguiente producto:
Para demostrar que los puntos A’, B’ C’ están alineados, vamos
a aplicar el teorema de Menelao al triángulo ABC. Es decir ver si vale
+1 el siguiente producto:
![]() .
.
Proyectando desde M sobre la recta AB, el triple producto es igual a este otro:
![]() , (*)
, (*)
donde se ha designado como s a la recta que pasa por
S y s’ a la que pasa por S’. Teniendo en cuenta que
los ángulos de a,a’; b,b’; c,c’ son rectos, los restantes ángulos son
áng(b’, a) = a; áng(c,
b’)=b ; áng(a’, c)=90-(a+b); áng(b, a’)= a; áng(c’,b)=b. Sustituyendo en (*) tendremos que m = ![]() =
= ![]() .
.
En conclusión: los puntos A’, B’ y C ’ están alineados.