Problema 90

 "ABC is an isosceles triangle. B=C=80 degrees. CF at 30 degrees to AC cuts AB

 in F. BE at 20 degrees to AB cuts AC in E. Prove angle BEF = 30 degrees".

ABC es un triángulo isósceles. Es < B= < C=80º. F está sobre AB tal que < ACF=30º.
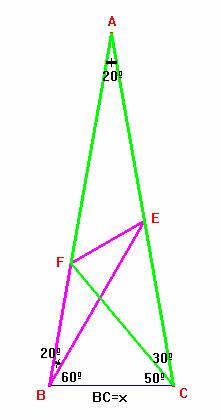
E está sobre AC tal que < ABE=20º. Demostrar que < BEF=30º

J.W. Mercer et al, Solutions to Langley's Adventitious Angles Problem (see Langley) , Mathematical Gazette, 11, 1923, pp321-323.

Sol:

Para demostrar que el ángulo BEF es igual a 30º probaremos que los triángulos obtusángulos ambos en F, ACF y BEF son semejantes. Como los ángulos en A y B son iguales a 20º, sólo bastará probar que los lados que lo forman son proporcionales entre sí.

De esta forma se tendrá que el ángulo en E del triángulo BEF será igual al ángulo C que es de 30º del triángulo ACF.

Por tanto, la tarea que nos queda será la de determinar la igualdad entre los cocientes siguientes:

AC/AF y BE/BF.

Usaremos un poco de trigonometría para nuestro objetivo:

Si llamamos BC= x, entonces:

;
AF= AC-x       Luego entonces:
 

Por otro lado,

;  
Y así se tendrá:

Veamos por fin que estas dos expresiones son idénticas:

Para ello:

2×cos40º×(1-2×sen10º)= 2×cos40º - 4×cos40º×sen10º = 2×cos40º - 2×(sen50º-sen30º)= 1,

 

 

c.q.d.