Problema 97.-

Las bisectrices internas de dos ángulos de un triángulo escaleno y la exterior del tercer ángulo cortan a sus respectivos lados opuestos en tres puntos que están alineados.

Solución de F. Damián Aranda Ballesteros profesor de Matemáticas del IES Blas Infante en Córdoba (18 de Mayo de 2003)

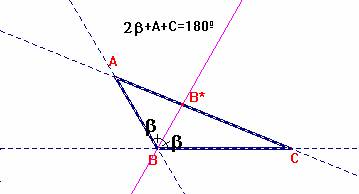
Teorema de la bisectriz interior de un triángulo.                                            Dado el triángulo ABC, trazamos la bisectriz interior correspondiente al ángulo B que corta al lado opuesto en el punto B*. Entonces se verifica la igualdad:                                              AB*/CB* = AB/CB .

Dem.-

Usando el teorema de los senos en los triángulos BB*C y ABB*, observamos las siguientes relaciones de igualdad:
senb/CB* = sen(A+b)/CB;

senb/AB* = sen(C+b)/AB;

Como quiera que A+2b+C=180º, entonces sen(C+b)=sen(A+b) y por tanto dividiendo ambas relaciones de igualdad obtenemos:

AB*/CB* = AB/CB

Teniendo en cuenta este resultado y el relativo a la tangente exterior podemos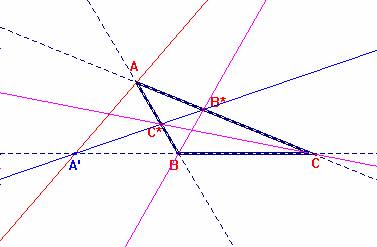

escribir los siguientes resultados:

AC*/C*B = AC/BC;

BA'/A'C   = AB/AC;

CB*/B*A =BC/AB;

De este modo, se verificará la relación exigida en el Teorema de Menelao (modo recíproco)  para que los punto A', B* y C* estén alineados. Es decir: