Problema 99.-
Un problema sobre semejanzas y paralelismo.
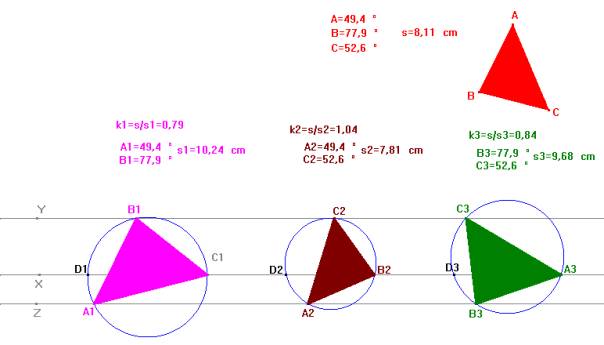
Construir un triángulo cuyos vértices están en tres paralelas dadas y que sea semejante a otro triángulo dado.
Solución de F. Damián Aranda Ballesteros profesor de Matemáticas del IES Blas Infante en Córdoba

Supongamos resuelto el problema y observemos a partir de dicha solución cómo puede realizarse la construcción.
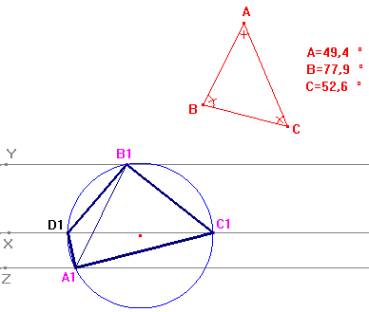Sea una cualquiera de las posibles soluciones A₁B₁C₁ y sea el punto D₁, punto que pertenece a una de las rectas, recta X, y a la circunferencia circunscrita al triángulo A₁ B₁ C₁. Desde este punto D₁ obtenemos las siguientes igualdades entre ángulos inscritos en la circunferencia

<A₁D₁C₁=<A₁B₁C₁=<B
<B₁D₁C₁=<B₁A₁C₁=<A

En definitiva, para un punto cualquiera D₁ situado en una de las rectas, p.e. recta X, giramos dicha recta alrededor del punto D₁ ángulos iguales a <B y <C, respectivamente y obtenemos así el triángulo D₁A₁B₁, cuya circunferencia circunscrita determina como segundo punto de intersección con la recta X, el tercer vértice C₁. Del mismo modo actuaríamos en todos los casos.