problema n° 60

Costruire il triangolo rettangolo di data ipotenusa c i cui cateti a e b hanno come media geometrica la metà dell'ipotenusa stessa: a*b = c²/4.

Construir el triángulo conociendo la hipotenusa c y tales que sus catetos a y b tengan como media geométrica la mitad de la hipotenusa, a*b= c²/4.

prof. Giovanni Porcellato

Liceo Scientifico "B. Pascal"

Merano

Alto Adige - Sudtirol

Italia

Costruzione e dimostrazione

Data l'ipotenusa AB si costruisce nell'ordine:

il punto medio M di AB,

la circonferenza g di centro M e raggio MA,

la retta perpendicolare per M ad AB;

il punto N, uno dei due punti d'intersezione tra la retta e la circonferenza g,

il punto medio O di MN,

la retta perpendicolare per O alla retta MN,

il punto C, uno dei due punti di intersezione tra la retta e la circonferenza g.

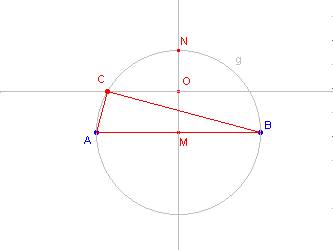
C è il terzo vertice del triangolo cercato.

Infatti se a, b e c sono rispettivamente le misure di BC, AC e AB l'area del triangolo rettangolo ABC, rettangolo perché C appartiene alla circonferenza g, può essere espressa sia in funzione di a e b sia in funzione di c:

area(ABC) = (a*b)/2 = c*(c/4)/2.

Quindi a*b = c²/4.

Construcción y demostración

Dada la hipotenusa AB, si construimos en el orden siguiente:

El punto medio M de AB,

La circunferencia g de centro M y radio MA,

La recta perpendicular por M a AB

El punto N, uno de los puntos de intersección de la recta y la circunferencia g,

El punto medio O de MN,

La recta perependicular por O a la recta MN,

El punto C, uno de los puntos de intersección la recta y la circunferencia g,

C es el tercer vértice del triángulo.

En efecto, sea a, b y c respectivamente la medida de BC, AC y AB.

El área del triángulo rectángulo debido a pertenecer C a la circunferencia g, puede ser

Expresado tanto en función de a y de b como de c:

Area (ABC) = (a*b)/2 = c*(c/4)/2, de lo que a*b = c²/4