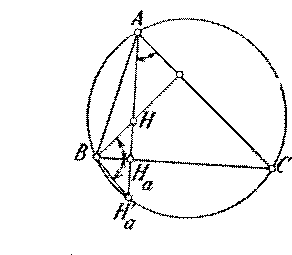
Problema 166

126.- Sean el círculo circunscrito a un triángulo ABC y H el punto de encuentro de las alturas. Si se prolonga la altura CG hasta F se tendrá: HG =GF.

(Traducción literal del editor. Se precisa que G es el punto de corte de la altura desde C con el lado AB o su prolongación. F es el punto de corte de la altura con la circunferencia circunscrita. )

André, M. Ph. (1920). Éléments de GÉOMÉTRIE Conformes aux programmes de baccalauréats (1re partie) de l'enseignement secondaire classique et de l'enseignement secondaire moderne. Contenant plus de mille problémés résolus et a resoudre.(Treinte-quatriéme edition). Paris, Librairie classique de FE André Guédon.E. Andre Fils Succeseur, 6 rue Casimir-Delavigne (près l'Odeon). (p. 83)

(El editor agradece a la Directora de la biblioteca de la Facultad de Ciencias de la Educación de la Universidad de Sevilla Ángela Arévalo la referencia (FRBNF31720368, http://catalogue.bnf.fr) en la Biblioteca Nacional de Francia de esta libro, ya que al ejemplar que poseo, le faltaba la página del año. !34 edidiciones!)

Préface.

Pendant bien des années, en présence d'intelligences plus o moins déeloppées, nous avons recherché avec perséverance les meilleurs procédés pour faire saisir aux élèves les vérités mathématiques. L'ouvrage que nous publions est le fruit de cette longue expérience dans l'enseignament des sciences exactes. Nous avons pu nous convaincre quíl est nuisible de faire apprendre aux élèves des definitions et des demostrations qui, sous le prétexte d'être faciles, n'ont pas le toute la rigueur mathématique désirable. La vérité est une: il est préférable de ne rien savoir que de mal savoir....

Prefacio:

Durante muchos años, en presencia de inteligencias más o menos desarrolladas, hemos buscado con preserverancia los mejores procedimientos para hacer comprender a los alumnos las verdades matemáticas. La obra que proponemos es el fruto de esta larga experiencia en la enseñanza de las ciencias exactas. Nos hemos podido convencer que es inútil hacer aprender a los alumnos las definiciones y demostraciones que, bajo el pretexto de ser fáciles, no tienen todo el rigor matemático deseable. La verdad es una: Es preferible no saber nada que saber mal...

Traducción libre del editor.

254 Teorema

El segmento de una altura desde el ortocentro al lado es igual en su extensión del lado al cincuncírculo; si A1H se extiende hasta encontrarse con el circuncírculo en H'1 entonces es H1 H'1 = H H1.

Johnson, R. A. (1929, 1960): Advanced euclidean geometry (Inicialmente titulado: Geometría moderna) Un tratado elemental sobre la geometría del triángulo y del círculo. Dover . New York.

Prefacio:

This book deals with the geometry of the triangle and the circle, as developed extensively in the nineteenth century by British and Continental writers. This geometry, based entirely on the elementary plane geometry of Euclid ....

Prefacio.

Este libro trata sobre la geometría del triángulo y del círculo, que se ha desarrollado extensivamente en el siglo diecinueve por escritores ingleses y continentales. Esta geometría, basada por completo en la geometría plana elemental de Euclies....

Nota del editor: Estos dos espléndidos y magníficos libros, son el primero de procedencia familiar. El segundo de procedencia amistosa. Es muy grato observar cómo Jonhson en 1929 hace una leve referencia a ¿posiblemente André(1920) ?

Traducción libre del editor:

Antes de empezar, me gustaría aclarar, que no pretendo presentar mi solución del enunciado 166.

Voy a usar como excusa este problema, para presentar dos enfoques distintos de la solución.

Ya el propio enunciado del editor muestra que multitud de textos lo incluyen y que muchos de ellos lo consideran como un resultado clásico.

De entre toda la bibliografía que tengo a mi alcance he elegido dos con los siguientes criterios:

a La solución más simple.

título: La Géométrie du Triangle

Autor: Trajan Lalesco

Edición: Jacques Gabay. Paris 2003

Réimpression autorisée de la 2^éedition publiée par la librairie vuibert. Paris 1952.

Localización: Nº 1.11 página 4

b La solución más compleja.

título: Géométrie projective. Cours, exercices et problèmes corrigés.

Autor: Jean-Claude Sidler.

Edición: Dunod. Paris 2000

2^éedition

Localización: Problema 8.4 página 113

LA SOLUCION SIMPLE

Los simétricos del ortocentro, respecto los lados, están sobre el círculo circunscrito

Figura Trajan Lalesco

Demostremos que . Basta observar que los ángulos y son iguales, pues ambos lo son al ángulo . El triángulo es así isósceles y en consecuencia, los puntos y son simétricos respecto a .

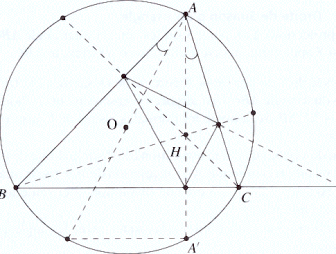
LA SOLUCION COMPLEJA

SIMETRICO DEL ORTOCENTRO. Demostrar que en un triángulo, el simétrico del ortocentro respecto a uno de los lados está sobre el círculo circunscrito al triángulo.

Figura de Jean-Claude Sidler

Sea el ortocentro de un triángulo y sea el simétrico de respecto a (figura). Las rectas y (respectivamente et ) que son simétricas respecto a , tienen sus puntos del infinito conjugados armónicos respecto a los puntos a los puntos del infinito , de las rectas , . Es fácil, entonces, verificar que la involución definida sobre la recta del infinito por el cuadrángulo puede escribirse como designamos con a la involución canónica y con la involución de puntos fijos , . Como intercambia y , la homografía es una involución, lo que demuestra que el haz de cónicas circunscritas al cuadrángulo contiene un círculo.

De entre las numerosas demostraciones elementales de este teorema, elegiremos una que raramente se suele dar:

Se apoya en las propiedades de la traslación; sea el punto diametralmente opuesto al vértice sobre el círculo . La recta es ortogonal a y el cuadrángulo es un paralelogramo; así la traslación de vector transforma en . El resultado esperado vendrá de la descomposición de la traslación en producto de simetrías, la una , tiene por eje el diámetro paralelo a , la otra de eje ; se tiene entonces:

ahora bien. es un punto del círculo , por ejemplo , y , el simétrico de respecto a .

Nota:

Este ejercicio 8.4 usa el resultado del ejercicio 7.24.1 sobre círculos en un haz. A su vez el 7.24.1 no sólo nos dirige al 7.7 sobre involuciones que permutan, usando además el teorema 6.1, tercer teorema de Desargues, y la proposición 3,4 sobre la composición de involuciones hiperbólicas. El 7.7 se apoya en el 7.5 sobre polaridad. El 7.5 usa el 7.1 sobre el cuadrángulo y conjugados ...

En fin, Sidler construye la solución de todos sus problemas usando un andamiaje que a su vez echa mano de todo lo que nos ha enseñado en el texto. El libro, demuestra casi todo y resuelve todos los ejercicios y problemas. ¡Uno aprende y profundiza en la geometría, aunque no quiera de un modo fácil y suficientemente actual.