La existencia de un triángulo con longitudes de las bisectrices prescritas.

Laurentiu Panaitopol , Petru Mironescu;

American Mathematical Monthly Vol 101, N 1 (Jan, 19949, 58-60 )

Dados tres números positivos arbitrarios m, n, p, ¿existe algún triángulo con bisectrices que midan n, n, p? La respuesta es SI.

Sin embargo el triángulo es único salvo isometría. Contrasta con otros resultados del triángulo.

Las longitudes de las medianas m,n, p deben satisfacer m< n+p y otras dos desigualdades cíclicas.

Las longitudes de las alturas deben satisfacer 1/m < 1/n + 1/p;así, m, n, p no pueden ser arbitrarias en estos casos.

las referencias tienen varias notas bibliográficas que muestran la amplia historia de este problema.

Brocard (Nouvelle Correspondance Mathemarique) propuso en 1875 tal construcción. ç

Van Den Berg ( Nieuw Archief voor Wiskunde,1889) lo resolvió con una ecuación de grado 16.

En 1896 Barbarin (Mathesis) la rebajó a 14, siendo irreducible en general. .

Mostró también que esta ecuación llega a ser cúbica cuando dos son iguales - por lo que

la construcción euclídea del triángulo es imposible. Ver más detalles en la bibliografía.

Si a, b y c son los lados, m, n y p son las bisectrices, y s el semiperímetro del triángulo, es:

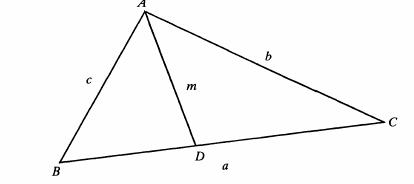
[1], con fórmulas similares para n y p.

Demostremos [1] por áreas:

Si AD es la bisectriz m, es 2S(ABC)= 2S(ABD) + 2S(ACD).

bc sen (A) = bm sen (A/2) + cm sen (A/2).

Luego es

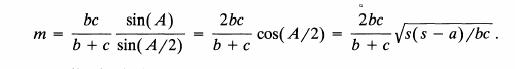
Se puede fácilmente chequear que:

[2]

Y, de [2], que:

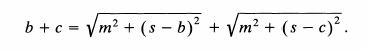 [3]

Tenemos dos igualdades relacionadas con c+a y a+b. Sustituyendo

            x= s-a,             y= s-b,             z=s-c  [4]

la relación [3] puede reescribirse como:

 [5]

donde  

Dados tres números arbitrarios reales positivos m,n,p, sea

  definida por:

Tomando en cuenta [5], es F(x,y,z)=(x,y,z). [6]

Siempre que x, y , z sean en [4] las longitudes de un triángulo cuyas bisectrices midan m, n, p. De manera inversa, si tenemos [6], entonces en el triángulo y+z, x+z, x+y la igualdad [3] es tal que (junto a las otras dos análogas) m debe ser dado por [1] en virtud de ser monótono el lado de [3] en la variable m. Aquí, el problema dado es equivalente a la existencia de un punto fijo para F

Existencia.

Dado  para no negativos u,v, se sigue que  donde

Señalemos que (0,0,0) no es punto fijo de F. Dado que K es un conjunto convexo compacto en R ² , y F es continuo, la existencia se sigue del teorema del punto fijo de Brouwer (ver, por ejemplo, (3)).

Unicidad.

Para v ≠ 0, u ≠ t, y   ,

Tenemos :  [7]

Para (x,y,z) ≠ (x’, y’, z’) [7] da:

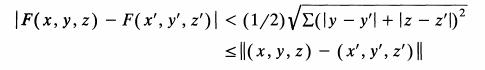 [8]

Donde ∑ denota la suma cíclica y ║   ║  denota la norma euclídea en R ³.

La unicidad se sigue de [8] inmediatamente.

Referencias: