Problema 163                  

      De forma análoga a como se obtienen los dos puntos de Fermat, construimos un cuadrado sobre cada uno de los lados de un triángulo  y unimos cada centro de estos cuadrados con el vértice opuesto (del lado sobre el que está el cuadrado) del triángulo.

        Así, se obtiene P_I cuando los cuadrados se construyen por el interior de los lados del triángulo:

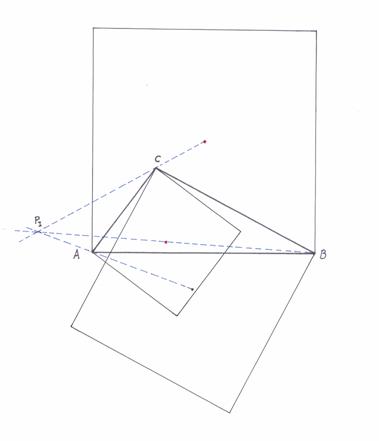Éste es el llamado INNER VECTEN POINT X(486) de la lista de Kimberling

Ver el problema 93 de esta colección, con soluciones de F. Damián Aranda Ballesteros,

Juan Carlos Salazar, con generalización, y de Saturnino Campo Ruiz (16-30 de abril de 2003)

Cuando los cuadrados se construyen por el lado exterior, se obtiene el punto P_E :

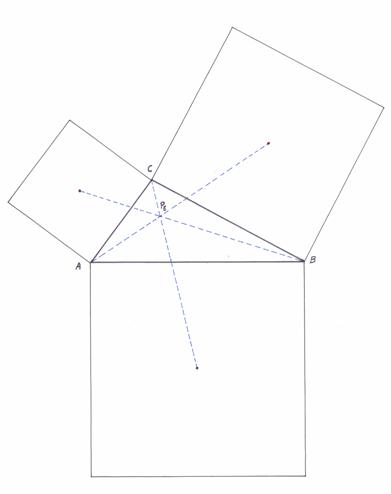        Este es el llamado VECTEN POINT X(485)

Pues bien P_I , P_E , y el centro de la circunferencia de los nueve puntos F

( ver problema 8 con soluciones de Saturnino Campo Ruiz y del editor (1-15 noviembre 2000)

,problema 12, con solución del editor (16-30 noviembre 2000)

,problema 15 sin resolver, 1-15 de diciembre de 2000)

problema 110 con Estudio de José Manuel Arranz San José, demostración según de Sortais, Y, R, (1997-2002), traducida por el editor, solución de Saturnino Campo Ruiz yTraducción del profesor Francisco Javier García Capitán)

siempre están alineados.

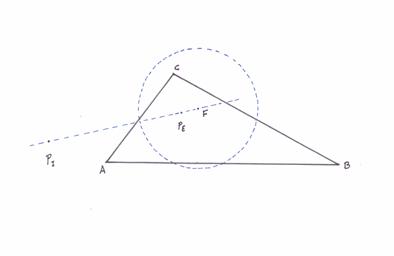Montes(2004): Propuesta personal.

José Montes Valderrama, profesor del Centro Público de Adultos ·"Triana", Sevilla .