Problema 111

Problema 111.- Los ruptores.

Solución de F. Damián Aranda Ballesteros profesor de Matemáticas del IES Blas Infante en Córdoba

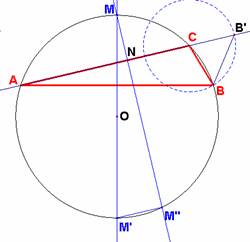
a)Si por el punto medio M de un arco de circunferencia que subtiende un triángulo ACB bajamos una perpendicular MN a la cuerda que comprenda el arco donde esté M ( en este caso AC), demostrar que AN = NC + CB.

Sol:

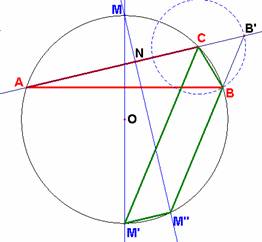
Al prolongar los segmentos MO y MN, determinamos en la circunferencia los puntos M' y M'', respectivamente. Así se verifica la igualdad entre los ángulos inscritos en la misma circunferencia <M'MM'' y <A, por estar formados por pares de lados perpendiculares entre sí.

De esta manera se dará la igualdad entre las cuerdas M'M'' y BC.

Si ahora prolongamos el lado AC y sobre esta recta determinamos el punto B' de modo que CB' = CB, entonces en el triángulo isósceles CB'B, se tiene que el ángulo B' es igual a C/2.

Si trazamos la bisectriz del ángulo C en el triángulo ABC, dicha bisectriz cortará a la circunferencia en M'. Por otro lado, el ángulo inscrito M''MA es igual a C/2.

Así, de este modo, los puntos B', B y M'' han de estar alineados ya que el ángulo exterior en B del triángulo ABB' deberá ser igual a C/2 + A.

Luego si prolongamos el lado B'B obtenemos la figura inscrita en la circunferencia BM''M'C que no es otra que un trapecio isósceles. Por tanto, los ángulos en la base son iguales y así, el ángulo inscrito CM'M'' = C/2 es igual también al ángulo inscrito CAM''.

Hemos probado así que el triángulo AB'M'', es isósceles con ángulos iguales en A y B' y así tenemos que el segmento NM'' es la mediatriz del mismo.

En definitiva, el punto N es el punto medio del lado AB', y así, AN = NB'.

Como NB' = NC + CB' = NC + CB, entonces:

AN = NC + CB .

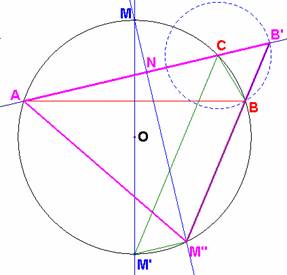
b) Dado un triángulo ABC, sea M el punto medio de CA. El segmento MQ tal que divide en dos mitades el perímetro del triángulo ABC, se denomina ruptor.

Construir Q, punto ruptor.

Sol:

Construimos el punto M₂ según hicimos en el apartado anterior. Para ello, sea M₁ el punto medio del arco de circunferencia que subtiende el triángulo ABC y ahora bajamos la perpendicular M₁M₂ a la cuerda AB.

En este caso, se tendrá que: AM₂ = M₂B + BC

y así el punto M₂ = Q, ya que el segmento MQ divide en dos mitades el perímetro del triángulo ABC.

MA + AQ = MC + CB + BQ.

c) Demostrar que QM es paralela a BN, bisectriz del ángulo B.

Sol:

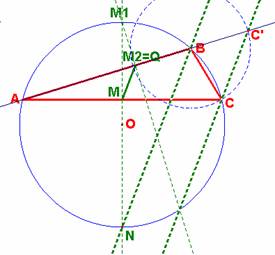
Según hemos visto en el apartado anterior, QM es la paralela media al lado CC' del triángulo ACC' , y como el lado CC' es a su vez paralelo a la bisectriz BN, tenemos que, en efecto, QM es paralela a BN, bisectriz del ángulo B.

d) Demostrar que los tres ruptores se encuentran en un punto, centro ruptor del triángulo.

Sol:

El centro ruptor R no es otro punto que el incentro del triángulo medial A'B'C' del inicial ABC, ya que por la construcción de los segmentos ruptores A'A'', B'B'' y C'C'', como paralelas a las bisectrices interiores de los ángulos A, B y C por los puntos medios A', B' y C', se tiene que dichos segmentos ruptores no son más que las bisectrices del triángulo medial A'B'C'.