Problema 111.- a) Si por el punto medio M de un arco de circunferencia que subtiende un triángulo ACB bajamos una perpendicular MN a la cuerda que comprenda el arco donde esté (en este caso AC), demostrar que AN = NC + CB.

b) Dado un triángulo ABC, sea M el punto medio de CA. El segmento MQ tal que divide en dos mitades el perímetro del triángulo ABC, se denomina ruptor. Construir Q el punto ruptor.

c) Demostrar que QM es paralela a BN, bisectriz del ángulo B.

d) Demostrar que los tres ruptores se encuentran en un punto, centro ruptor del triángulo.

Solución  de Saturnino Campo Ruiz, profesor de Matemáticas del I.E.S. Fray Luis de León (Salamanca)

.-  a) El punto N buscado, por cumplir que AN = NC + CB es tal que AN + (NC+CB) = 2 AN = b + a, es decir, AN = ½(b+a); el punto N puede obtenerse llevando a continuación de C el segmento CB y tomando el punto medio del segmento resultante. Trazando la mediatriz m de AB’ hallamos el punto N y el punto M, corte de la mediatriz con el arco AB que subtiende el triángulo.

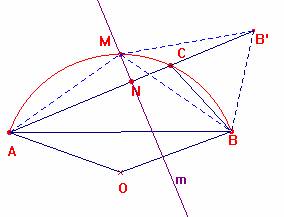Lo que queremos probar es que M es el punto medio del arco BCA. Bastará que probemos que los segmentos BM y  AM son iguales. En efecto: Por ser m mediatriz de B’A, el punto M equidista de los extremos, y los ángulos MB’C  y  CAM son iguales. También son iguales los ángulos CBM y CAM por abarcar el mismo arco, por tanto, a=áng(MB’C) =áng(MBC). Por último el triángulo B’MB es isósceles, pues son iguales los segmentos CB’ y CB (por construcción) y los ángulos MB’C y  MBC, de donde se concluye que BM =B’M = AM y M es el punto medio del arco.

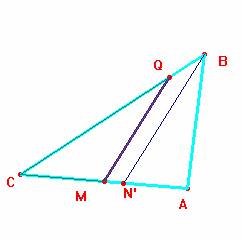b) El punto Q debe verificar que perím(CQM) = perím(QMAB) = ½ perím(ABC), lo que nos conduce a la relación CQ = AB +QB, ya que M es el punto medio de AC. El punto Q buscado es el punto N del apartado anterior. Puede construirse como allí: se busca la circunferencia que circunscribe ABC. Se halla el punto M (mediatriz de AB y corte con la circunferencia) y desde M se traza la perpendicular.

Más sencillo es llevar el segmento BA en la prolongación de CB, a continuación de B y hallar el punto medio. Así se determina Q.

c) Tracemos por B un segmento paralelo a QM, sea éste BN’. Queremos probar que N’ = N, esto es, que BN’ es la bisectriz y por tanto QM es paralelo a ella.

De la semejanza de los triángulos de la figura se tiene: por construcción CQ= ; CM = ½ b, luego CN’= CM = . Sea ahora BN la bisectriz de B.

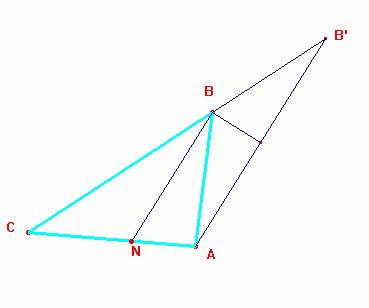 El segmento BB’ = BA se lleva a continuación de CB. Por ser isósceles ABB’ la altura sobre AB’ es la bisectriz exterior de B, que es perpendicular a la interior BN, y por tanto BN  es paralelo a AB’. Aplicando el teorema de Thales resulta: CB’/CA = CB/CN de donde CN = CN’, luego N=N’ como queríamos probar.

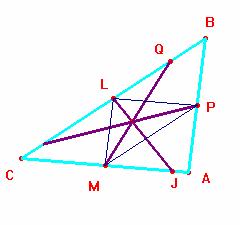d) Sean L, M y P los puntos medios de los lados a, b y  c respectivamente.

El triángulo mediano (= formado tomando los pies de las medianas de ABC como vértices) es semejante a ABC y de lados paralelos. Si LJ (segmento ruptor) es paralelo a la bisectriz del ángulo en A, como éste es igual al ángulo en L y ambos tienen sus lados paralelos, LJ es la bisectriz de L. Así pues los tres ruptores son las bisectrices del triángulo mediano y concurren en un punto, como se quería demostrar.