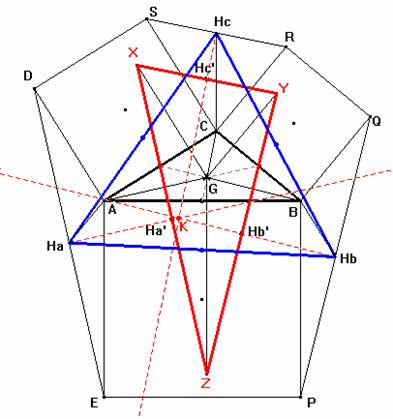
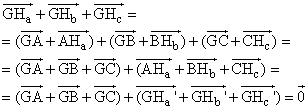Problema 112.- Cuadrados sobre un triángulo.
Sobre los lados de un triángulo arbitrario ABC se construyen hacia el exterior cuadrados. Se tiene:
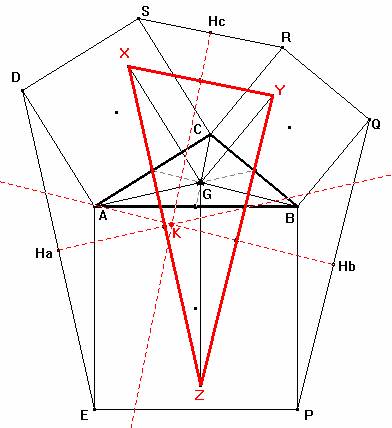
(1): Los vértices PQRSDE de los cuadrados diferentes de los del triángulo ABC forman un hexágono; las mediatrices de sus lados pasan alternativamente por el circuncentro U de ABC y por un segundo punto K.
(2): Los puntos medios de los segmentos cuyas mediatrices se intersecan en K, Ha, Hb y Hc, forman un triángulo cuyo baricentro es G, coincidente con el baricentro de ABC.
(3): Los triángulos Ha Hb Hc y ABC son homológicos en el sentido de Desargues, y su centro de homología es H, ortocentro de ABC.
(4): Las mediatrices HaK HbK y HcK son paralelas a las medianas AG, BG y CG de ABC
Sol F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba.
Para probar las anteriores proposiciones haremos uso del siguiente resultado fundamental que a continuación exponemos en forma de Lema.
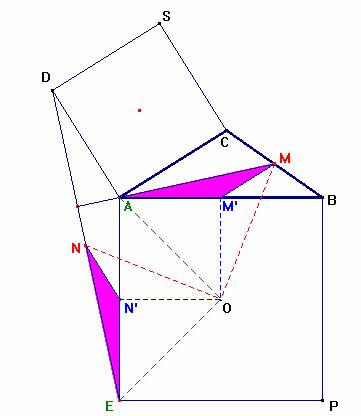
Lema Sobre los lados AB y AC de un triángulo arbitrario ABC
se construyen hacia el exterior los cuadrados ABPE y ACSD. Sean M y N, respectivamente
los puntos medios de BC y ED.
Entonces AM es perpendicular a ED y AN es perpendicular a BC.
Dem.-
| |
Sean M’ y N’ los puntos medios de los lados AB y AE respectivamente. Veamos la congruencia que existe entre los triángulos AMM’ y ENN’. Para ello, observamos la igualdad dada entre los lados AM’ y N’E por un lado (= la mitad del lado del cuadrado ABPE) y MM’ con NN’ por otro (= la mitad del lado del cuadrado ACSD) así como el ángulo <ENN' = <AM'M, al venir este ángulo dado por dos pares de lados perpendiculares entre sí. Por tanto el ángulo N’EN es igual al ángulo M’AM. Como los lados N’E y M’A son perpendiculares entre sí también lo serán los otros lados AM y EN. |
| En definitiva, AM y ED son perpendiculares entre sí. De igual manera se probaría que AN y BC serían perpendiculares. |
|
Veamos cómo este Lema explica o justifica en gran parte todas las proposiciones enunciadas.
| |
Si llamamos Ha , Hb y Hc a los puntos medios de los segmentos que no son lados de los cuadrados construidos exteriormente al triángulo inicial dado ABC, tenemos que, según el Lema probado, las semirrectas HaA , HbB y HcC son perpendiculares a los lados a, b y c, respectivamente. Por tanto dichas rectas son las tres alturas del triángulo ABC y concurren en el punto H, ortocentro del mismo. De este modo, los triángulos Ha Hb Hc y ABC son homológicos en el sentido de Desargues, y su centro de homología es H, ortocentro de ABC. (Prop iii) |
| |
Sea el punto G, baricentro del
triángulo ABC, y consideramos los vectores Al trasladar según aquellos vectores los triángulos ADE , BPQ y CRS todos concurren en G. Obsérvese que los ángulos en A, B y C de los triángulos primeros miden respectivamente, 180º-A, 180º-B y 180º-C. Luego en G suman 360º. Según esta traslación los puntos Ha, Hb y Hc se transforman en los puntos medios del triángulo XYZ y las mediatrices de los lados no son otras que las mediatrices del triángulo XYZ que concurren en K, circuncentro del mismo. (Prop i) |
| |
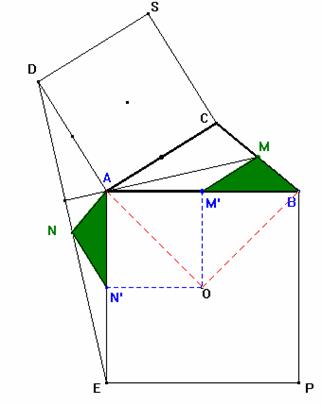
Volvamos otra vez
a la figura inicial que nos sirvió par ilustrar el Lema. Los triángulos
señalados en color verde son congruentes ya que coinciden dos lados
y el ángulo que ambos determinan. Estos elementos son los siguientes: Lado MM'= NN' <MM'B = <NN'A Por tanto también son iguales los lados MB y AN o lo que es lo mismo AN=1/2×a. Este último resultado va a tener una importancia a la hora de probar la (prop ii) como ahora veremos a continuación. El triángulo XYZ tiene como baricentro el mismo punto G, baricentro
del triángulo ABC ya que los puntos medios Ha', G e Y son
colineales al ser Ha'G perpendicular al lado BC, luego paralelo
al lado BD (o CR). Por tanto como GY es paralelo a BD, resulta que,
en efecto, los puntos Ha', G e Y son colineales. Además
por el último resultado probado anteriormente resulta que: De igual manera probaríamos que: Hb'G = 1/2 GX = 1/2 b. Hc'G = 1/2 GZ = 1/2 c. Por tanto, G es también el baricentro del triángulo XYZ y se verificará
que Veamos por fin, que G es también el baricentro del triángulo Ha
Hb Hc. Bastará probar para que Y esa igualdad es cierta sin más que observar que la suma anterior
se descompone así: (prop ii) |
| |
Saludos de F. Damián Aranda Ballesteros.