Problema 112.- Cuadrados sobre un triángulo.
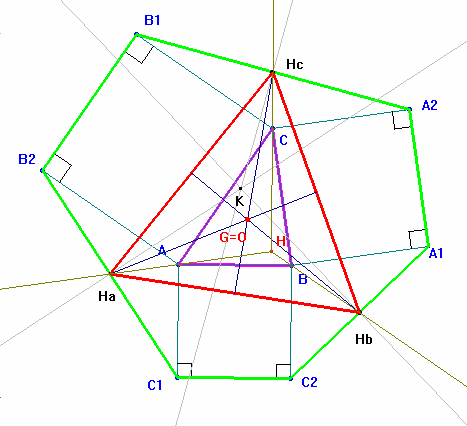
Sobre los lados de un triángulo arbitrario ABC se construyen hacia el exterior cuadrados. Se tiene:
Los vértices A1 A2 B1 B2 C1 C2 de los cuadrados diferentes de los del triángulo ABC forman un hexágono; las mediatrices de sus lados pasan alternativamente por el circuncentro U de ABC y por un segundo punto K.
Los puntos medios de los segmentos cuyas mediatrices se intersecan en K, Ha, Hb y Hc, forman un triángulo cuyo baricentro en S, coincidente con el baricentro de ABC.
Los triángulos Ha Hb Hc y ABC son homológicos en el sentido de Desargues, y su centro de homología es H, ortocentro de ABC.
Las mediatrices de HaK, HbK y HcK son paralelas a las medianas AS, BS y CS de ABC.
Solución de Saturnino Campo Ruiz (profesor del IES Fray Luis de León de Salamanca).- Vamos a comenzar viendo una curiosa propiedad de los triángulos construidos exteriormente al dado, que va a traer importantes consecuencias para la solución del problema.
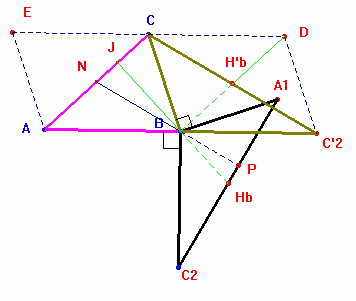
La mediana BHb del triángulo BA1C2 es la altura desde B del triángulo ABC y la mediana BN de ABC es la altura BP del triángulo BA1C2.
En efecto, un giro de 90º centrado en B del triángulo externo nos lo transforma en el triángulo BCC’2.
Como BC’2 es igual a AB y BC es común, puedo construir el triángulo BC’2D que es el propio ABC trasladado.
Construyo paralelogramos iguales ABCE y BC’2DC a partir de estos dos triángulos.
De las propiedades de las diagonales del paralelogramo deducimos que el segmento BH’b es paralelo e igual al segmento AN, y por tanto, que la mediana del triángulo externo BA1C2 es perpendicular al lado AC: es la altura desde B del triángulo ABC.
De otra parte, el lado C’2C es paralelo a la mediana BN, lo que significa que la recta soporte de esta mediana es perpendicular al lado A1C2, como pretendíamos demostrar.
De esta doble propiedad concluimos las partes 3ª y 4ª del problema, pues las rectas de la forma HrR, son las alturas del triángulo ABC que concurren en el ortocentro del mismo, el punto H, lo cual prueba que los triángulos Ha Hb Hc y ABC son homológicos (ver figura final).
Por otro lado, las mediatrices de los lados del hexágono que no son lados del triángulo, son paralelas a las alturas sobre ellos de los triángulos externos, y como estas son soporte de las medianas del triángulo dado, resulta de inmediato que aquellas mediatrices son paralelas a estas medianas.
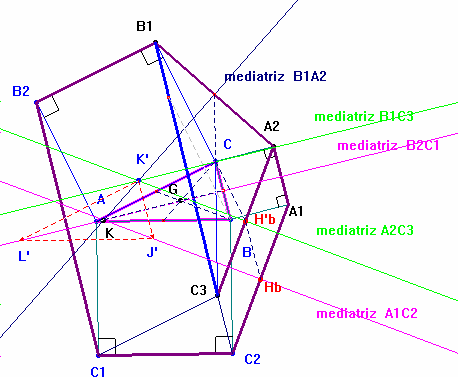
Vamos a probar el primer punto.
Las mediatrices de los lados del hexágono que son iguales a lados del triángulo, son evidentemente, las mediatrices de éste y se cortan en el circuncentro U del mismo.
Que las mediatrices de los otros lados son concurrentes en K no es tan evidente.
En primer lugar traslademos convenientemente los segmentos A1C2 y B2C1 hasta formar un triángulo con B1A2..
Las mediatrices de este triángulo (el B1A2C3) concurren en K’.
A partir de ellas vamos a trazar las de los lados A1C2 y B2C1.
Para hallar la del primer segmento, localizo en K’ el vector CB (que es el que realiza la traslación de A2C3 a A1C2 ), y trazo por su extremo una paralela a la mediatriz de A2C3.
Para hallar la segunda localizo en K’ el vector CA y trazo por su extremo una paralela a la mediatriz de B1C3.
Uniendo K’ con los extremos de estos vectores, vemos que hemos reconstruido el triángulo inicial ABC y que las mediatrices de los lados del hexágono (que, según vimos, son paralelas a las medianas de ABC) son las medianas de este triángulo y concurren en el punto K: su baricentro.
Veamos que C es el baricentro de B1A2C3 .
CB1 es perpendicular a AC, por tanto es paralelo a la altura de ABC sobre este lado (cuya prolongación pasa por el punto medio Hb de A1C2 )
La traslación de A1C2 a A2C3 según el vector BC lleva esta altura al segmento CB1, y el punto medio Hb al punto medio H’b de A2C3.
Así pues CB1 es una mediana.
Que CC3 lo es, ya está probado.
Es una altura de ABC, cuya prolongación pasa por Hc, punto medio de A2B1. Y ya necesariamente CA2 es la tercera mediana.
Si C es el baricentro verifica que CA2 + CB1 + CC3 = 0, (suma vectorial), es la propiedad que caracteriza al baricentro o, lo que es equivalente, 3·OC = OA2 + OB1 + OC3.
Vamos a utilizar esta propiedad para finalmente, probar que los dos triángulos homológicos tienen el mismo baricentro.
El baricentro de ABC se obtiene tomando la media aritmética de las coordenadas de los tres puntos.
Los puntos Hm son puntos medios de segmentos: sus coordenadas son también media aritmética de coordenadas de los extremos.
Así pues, el baricentro del triángulo HaHbHc es el punto G’, cuyas coordenadas son la media aritmética de las coordenadas de los vértices del hexágono:
6·OG’ =2· (OHa + OHb+ OHc) =OB2+OC1+OC2+OA1+OA2+OB1.
Tomando como origen de los vectores el punto G y observando la figura tenemos:
GC1 = GA + CC3 ; GC2 = GB + CC3 ; GA1 = GB + CA2 ; GA2 = GC + CA2 ; GB1 = GC + CB1 y GB2 = GA + CB1.
Sumando todo resulta 6·OG’= 2·(GA + GB + GC) + 2·( CA2 + CB1 + CC3) = 0 (vector nulo), eso sólo puede ser si O (= G) = G’. Cqd.