1 de Octubre de 2003-15 de Octubre de 2003

Problema 113

108.- Si dos triángulos tienen respectivamente iguales dos pares de lados, que comprenden ángulos desiguales, el ángulo mayor está opuesto al lado mayor.

Severi, F (1952): Elementos de Geometría (I). Con 220 figuras. Labor. S.A. Barcelona. (p. 110)

Solución:

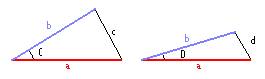
Si utilizamos el teorema del coseno,

c²-d²=2abcosD-2abcosC=2ab(cosD-cosC); con C>D

Si analizamos ahora en los distintos valores posibles de esa igualdad vemos que:

Cuando C es menor que 90º, cos D es siempre mayor que cos C y por tanto el segundo miembro de la ecuación es positivo y el primero también habrá de serlo, por lo que c>d.

Cuando C es mayor que 90º y D menor que 90º, cos D es positivo y cos C es negativo por lo que el segundo miembro de la igualdad es positivo así como el primero, por lo que c>d.

Por último, cuando los dos son mayores que 90º y por ser de un triángulo menores que 180º, pero ahora ambos cosenos son negativos pero el valor absoluto de cos C es mayor que el valor absoluto de cos D y por tanto nuevamente el segundo miembro de la ecuación es positivo y como el primero ha de serlo, siempre c>d si C>D y por tanto la respuesta al enunciado es que sí es verdad que al ángulo mayor le corresponde el lado mayor.