Problema 114.-

Dado un triángulo ABC, se tiene que los tres ángulos ACO, OCP y PCB son iguales, siendo CO la mediana, CP la altura del triángulo ABC, y O, P puntos del segmento AB. Indagar

a) ¿qué tipo de triángulo es ACO? ,

b) ¿qué tipo de triángulo es COB?

c)¿qué tipo de triángulo es ACB?.

Kurina, F. (2003): Geometry-The resource of opportunities. Documento presentado a Third Conference of the European Society for Research in Mathematics Education 28 February - 3 March 2003 in Bellaria, Italy (CERME, 2003)

Solución de F. Damián Aranda Ballesteros.

Del enunciado propuesto se deduce que el punto P, pie de la altura relativa al vértice C, ha de estar en el interior del segmento AB. Por tanto, la situación posible para nuestro empeño será la siguiente:

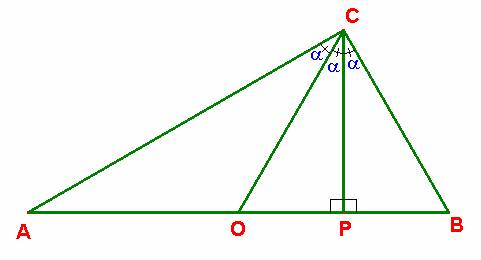
De dicha situación se deduce que el triángulo COB es isósceles siendo OP la mitad de OA. También se desprende que CO es la bisectriz del ángulo <ACP en el triángulo rectángulo ACP.
Por tanto, se verifica en este triángulo ACP que:

OP/OA =  CP/CA o lo que es lo mismo,  1/2 = sen<CAP. Por tanto <CAP = 30º.

Así tenemos que 2a=60º y a =30º. En definitiva se tiene que:

<ACB=90º y el triángulo ACB es rectángulo en C de ángulos en A=30º y B=60º.

En resumidas cuentas, el triángulo ACO es isósceles de ángulos iguales a 30º. El triángulo COB es también isósceles de ángulos iguales a 60º, y por tanto equilátero,  y el triángulo ABC es rectángulo en C y de ángulos 30º y 60º.