Problema 114.-
|
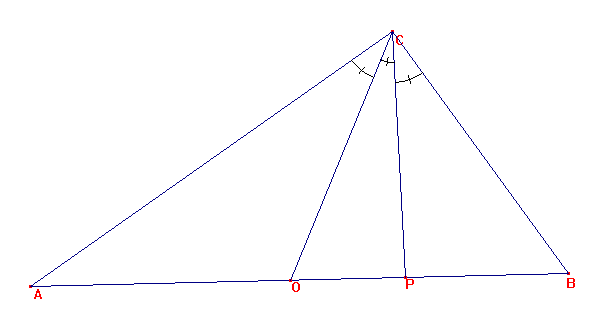
Dado un triángulo ABC, se tiene que los tres ángulos ACO, OCP y PCB son iguales, siendo CO la mediana, CP la altura del triángulo ABC, y O, P puntos del segmento AB. Indagar a) ¿qué tipo de triángulo es ACO? , b) ¿qué tipo de triángulo es COB? c)¿qué tipo de triángulo es ACB?. |
Kurina, F. (2003): Geometry-The resource of opportunities. Documento
presentado a Third Conference of the
European Society for Research in Mathematics Education 28 February - 3 March
2003 in Bellaria, Italy (CERME, 2003)(Modificado por el editor)
Con permiso de su autor, Frantisek Kurina Univerzita Hradec Králové CZECH
REPUBLIC
Solución ofrecida por el editor, a partir de alguna indicación de la comunicación del profesor Kuirna .

Del enunciado se tiene que < ACO = < OCP = < PCB = m.
Así se deduce que :
1.- < COP = 90 - m = < CBP.
2.- El triángulo COB es inicialmente isósceles y PB= PO= p.
3.- AO = 2p
4.- Al ser CO bisectriz del triángulo ACP, se tiene que OA / AC = OP / PC, por las propiedades de la bisectriz interna (ver problema 1 de esta página web).
Luego es 2p / AC= p / PC. Es decir, que AC= 2 PC.
. 5.- Tracemos la altura del triángulo AOC relativa al vértice O.
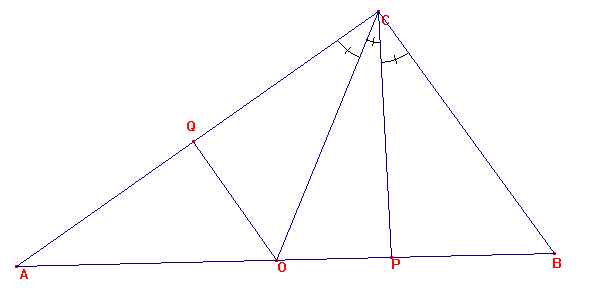
6.- Observemos los triángulos COQ y CBP. Ambos son rectos en Q y P, además de tener igual el ángulo en C siendo m. Luego sus tres ángulos son iguales. Como además tienen los lados CO y CB iguales, ambos triángulos son congruentes, y es CQ=CP , de hecho el giro de centro C y ángulo 2m transforma uno de ellos en el otro.
7.- De los apartados 4.- y 6 anteriores se tiene que AQ= AC-CQ = 2PC - CQ= 2PC-PC= PC= QC.
Es decir, que OQ no sólo es la altura de AOC, sino que también es su mediana.
8.- De lo anterior se desprende pues que los triángulos AQO y CQO tienen QO común y AQ=QC por lo que son rectángulos simétricos respecto a OQ, y por ello < OAQ= <OCQ . Por ello, se tiene la respuesta a a) por tanto, <OAC = < OCQ=m. ACO es isósceles.
9.- Observemos ahora el ángulo < CBA= < CBP = 90-m. De ello tenemos que :
< CAB + < ACB + < CBA = (m) + (3m) + (90- m) = 90 + 3m =180, de donde se tiene que 3m = 90, y, por último, m = 30.
10.- El triángulo COB tiene todos sus ángulos iguales, por lo que la respuesta a b) es que es equilátero.
11.- Después de lo anterior, se deduce que ACB es rectángulo, respondiendo a c)
Hasta aquí la solución ha sido aportada en principio por indicaciones de la comunicación al CERME3 de Italia del profesor Kurina.
Pequeñas implicaciones geométricas del problema aportadas por el editor.
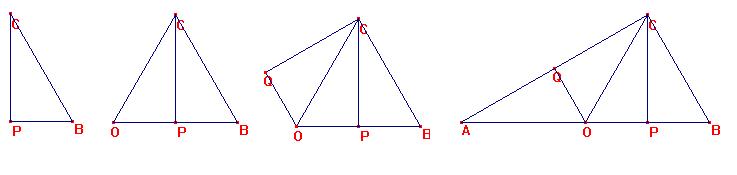
El triángulo CPB es "generador" del ACB. Si tenemos CPB y tomamos su simétrico respecto a CP, se transforma en CPO.
De esta manera tenemos construido OCB (triángulo equlátero).
Si luego transformamos CPO respecto a CO tomando su simétrico, tendremos el triángulo OCQ, y el cuadrilátero OQCB.
Si por último transformamos OCQ respecto a OQ tomando de nuevo su simétrico, OQA, tendremos por fin ACB.
Además, el triángulo ACB es semejante al CPB de razón de semejanza 2, ya que:
AB= 2OB= 2CB; AC= 2QC= 2 CP, CB= OB=2PB.
Esta última propiedad nos lleva a otra configuración del triángulo, teniendo lugar una descomposición del mismo de nuevo
en cuatro triángulos congruentes con PCB.
Si llevamos un triángulo MTR congruente con el CPB sobre ACB coincidiendo loa ángulos rectos, tendremos que
el punto T coincidirá con C, y R con el punto medio de AC ( Q) , y M con el punto medio de CB.
Por ello, será TM = AO = OB , con las consecuencias geométricas subsiguientes:
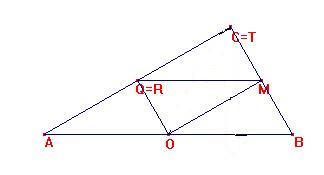
De nuevo ACB se descompone en cuatro triángulos semejantes a él mismo.
Además, OQTM es rectángulo.
AOMQ es paralelogramo.
OQCB y QMBA son trapecios.
Ricardo Barroso Campos. Editor de trianguloscabri.
Didáctica de las Matemáticas.
Universidad de Sevilla.