Problema 114.-

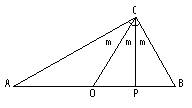
Dado un triángulo ABC, se tiene que los tres ángulos ACO, OCP y PCB son iguales, siendo CO la mediana, CP la altura del triángulo ABC, y O, P puntos del segmento AB. Indagar

a) ¿qué tipo de triángulo es ACO? ,

b) ¿qué tipo de triángulo es COB?

c)¿qué tipo de triángulo es ACB?.

Kurina, F. (2003): Geometry-The resource of opportunities. Documento presentado a Third Conference of the
European Society for Research in Mathematics Education 28 February - 3 March 2003 in Bellaria, Italy (CERME, 2003)(Modificado por el editor)

Con permiso de su autor, Frantisek Kurina Univerzita Hradec Králové CZECH REPUBLIC

Solución:

Llamando b a CB y c a AO=OB,

Si utilizamos el teorema del seno sobre los triángulos ACB y OCB, obtenemos:

OCB: c/sen(2m)=b/sen(90-m)=b/cos(m)

ACB: 2c/sen(3m)=b/sen(90-2m)=b/cos(2m)

Si normalizamos y hacemos b=1, y igualamos las c obtenemos:

sen(2m) 2 cos(2m) = sen (3m) cos (m);

el primer miembro es usando las fórmulas de adicción de razones trigonométricas igual a :

sen(4m)=sen(m) cos(3m) + sen(3m) cos (m) = sen (3m) cos (m) por lo que

sen(m) cos (3m) = 0 y esto solo ocurre si m=0 o 180º, que entonces toda la figura sería una recta o bien si m= 30º, y entonces;

ACB sería un triángulo rectángulo de ángulos 90, 60 y 30

OCB sería un triángulo equilátero de lado CB o AB/2

AOC sería un triángulo isósceles de lados AO=CO y AC y de ángulos iguales iguales a 30º y ángulo desigual igual a 120º.