Problema 114.- Dado un triángulo ABC, se tiene que los tres ángulos ACO, OCP y PCB son iguales, siendo CO la mediana, CP la altura del triángulo ABC, y O, P puntos del segmento AB. Indagar
a) ¿qué tipo de triángulo es ACO? ,
b) ¿qué tipo de triángulo es COB?
c)¿qué tipo de triángulo es ACB?
Solución de Saturnino
Campo Ruiz, profesor de Matemáticas del I.E.S. Fray
Luis de León (Salamanca) 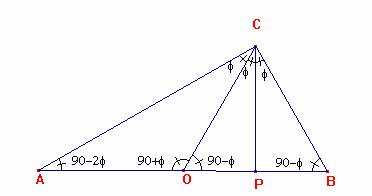
- Siendo CP
una altura, de la igualdad de los ángulos OCP
y PCB se deduce que el triángulo OCB es isósceles y esta altura es una bisectriz del
mismo, por tanto AO = c/2 y OP
= PB = c/4, CO = a. El resto de ángulos son los que aparecen
en la figura. Como es habitual a = BC; b = AC y c = AB. En el
triángulo PCB se tiene senf =
![]() , de donde
c = 4asenf, y en el triángulo AOC,
, de donde
c = 4asenf, y en el triángulo AOC, 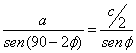 ,
en esta última, sustituimos c, y obtenemos
,
en esta última, sustituimos c, y obtenemos ![]() , o sea,
, o sea,
![]() = 1/2.
La única solución posible para este triángulo es que sea 2 f = 60 º. Así pues,
el triángulo ABC rectángulo en C y sus ángulos agudos son de
30º y 60º respectivamente (parte c). El triángulo ACO
es isósceles (parte a), pues AO =a=c/2=OC. Finalmente, el triángulo
COB es equilátero (parte b).
= 1/2.
La única solución posible para este triángulo es que sea 2 f = 60 º. Así pues,
el triángulo ABC rectángulo en C y sus ángulos agudos son de
30º y 60º respectivamente (parte c). El triángulo ACO
es isósceles (parte a), pues AO =a=c/2=OC. Finalmente, el triángulo
COB es equilátero (parte b).