Problema 116.-

Se tiene un triángulo ABC. Consideremos su circunferencia circunscrita y sea D un punto de la misma.

Con centro en A y radio AD se traza una circunferencia Ca.

Con centro en B y radio BD se traza una circunferencia Cb.

Con centro en C y radio CD se traza una circunferencia Cc.

Ca y Cb se cortan en D y X; Ca y Cc se cortan en D e Y; Cb y Cc se cortan en D y Z.

Demostrar que los puntos X, Y y Z están alineados.

Olimpiada Canguro 2003 . Problema propuesto por el profesor esloveno Matija Pretnar en la concentración de Francia (verano de 2003).

Solución de F. Damián Aranda Ballesteros

X, Y y Z son los puntos simétricos respecto del punto D de los pies X',Y' y Z' de las perpendiculares trazadas por el punto D hacia los respectivos lados del triángulo ABC. Como quiera que los puntos X', Y' y Z' están alineados (Recta de Simson) también lo estarán los puntos X, Y y Z.

Veamos todo esto con mayor detalle.

Lema 1.-
X, Y y Z son los puntos simétricos respecto del punto D de los pies X',Y' y Z' de las perpendiculares trazadas por el punto D hacia los respectivos lados del triángulo ABC.

Dem.- 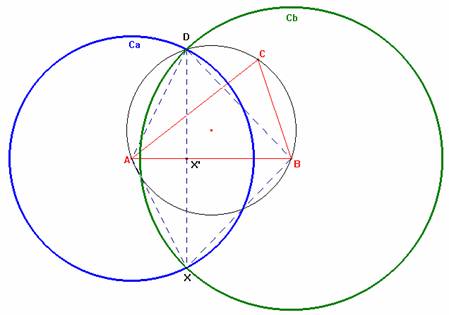Veamos esto para el caso de X y X'. Por la simetría de la construcción hecha, resulta que los segmentos DX y AB son perpendiculares y así se tiene que X' es el punto medio del segmento DX, o lo que es lo mismo X es el simétrico de D respecto del punto X'.

Lo mismo sucederá con los puntos Y y Z, respectivamente.

Lema 2.-
Los puntos X', Y' y Z' están alineados (Recta de Simson).

Dem.- Veamos una demostración clásica de este hecho.

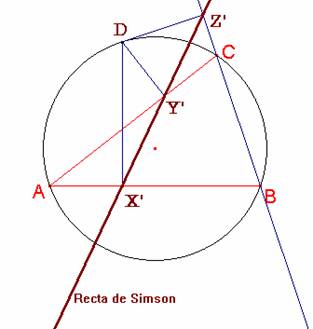Para probar que X', Y' y Z' están alineados veamos que los ángulos <AY'X' y <Z'Y'C son iguales. Para ello sigamos las igualdades entre los siguientes ángulos:

i)                    <ADC = 180º-<B
por tratarse de ángulos opuestos en el cuadrilátero inscriptible ABCD.

ii)                   <X'DZ' = 180º-<B
por tratarse de ángulos opuestos en el cuadrilátero inscriptible X'DZ'B.

iii)                 Luego <ADC = <X'DZ' y así sucede que:
<ADX' = <CDZ'

iv)                 <ADX'= <AY'X' ya que A, X',Y' y D son puntos de la circunferencia de diámetro AD.

v)                  <CDZ' = <Z'Y'C,  pues D,Y',C y Z' son puntos de la circunferencia de diámetro CD.

vi)                 En definitiva, <AY'X' = <Z'Y'C,  c.q.d.

Prop.-
Los puntos X, Y y Z están alineados.

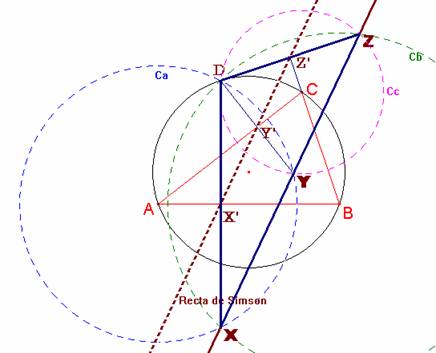Dem.- Teniendo en cuenta el Lema 1, los puntos X', Y' y  Z' son los puntos medios de los segmentos DX, DY y DZ.

Por otro lado, tenemos que los puntos X', Y' y Z' están alineados por el Lema 2.  

Uniendo ambos hechos convendremos, por fin, que los puntos X, Y y Z están también alineados, quedando la recta de Simson como la paralela media en el triángulo DXZ .