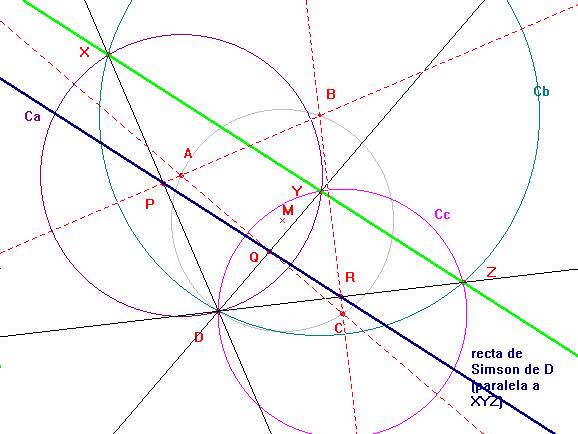
Problema 116.- Sobre un punto de la circunferencia circunscrita.

Se tiene un triángulo ABC. Consideremos su circunferencia circunscrita y sea D un punto de la misma.

Con centro en A y radio AD se traza una circunferencia C_a.

Con centro en B y radio BD se traza una circunferencia C_b.

Con centro en C y radio CD se traza una circunferencia C_c.

C_a y C_b se cortan en D y X; C_a y C_c se cortan en D e Y; C_b y C_c se cortan en D y Z.

demostrar que los puntos X, Y y Z están alineados.

Olimpiada Canguro 2003 . Problema propuesto por el  profesor esloveno Matija Pretnar en la concentración de Francia (verano de 2003).

Solución Saturnino Campo Ruiz, profesor de Matemáticas del I.E.S. Fray Luis de León (Salamanca) (16 de octubre de 2003)-

De la observación de la figura se deduce lo siguiente:

1. La recta DX, es el eje radical de las circunferencias C_a y C_b, por tanto es perpendicular a AB (segmento de los centros).
2. De igual modo, las rectas DY  y DZ son perpendiculares a los lados AC y BC respectivamente.
3. Los puntos P, Q y R de intersección de esas rectas con los lados del triángulo forman la recta de Simson del punto D.

Vamos a demostrar que los puntos del enunciado están alineados en una recta paralela a la recta de Simson. Para ello observamos los triángulos DXZ  y DXY. El primero está circunscrito en C_b y el segundo en C_a. Para DXZ  tenemos que BC  y DZ son perpendiculares, así como AB y DX. Esto es, BC y AB  son mediatrices de DXZ, por tanto R y P son los puntos medios de los lados DZ y DX, o lo que es igual, PR  es paralelo a XZ, más aún, es su paralela media.

Si consideramos el triángulo DXY, el mismo razonamiento nos lleva a que PQ  es la paralela media de XY.  La alineación de P, Q y R  (recta de Simson de D) nos lleva a concluir la de X,Y  y Z.