Problema 118.- Cuatro puntos alineados
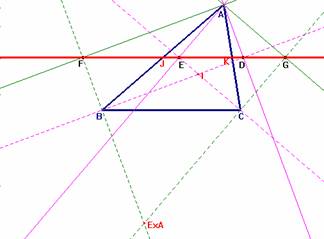
137.- Si en un triángulo cualesquiera ABC se trazan las bisectrices exteriores e interiores de los ángulos B y C, y luego se bajan desde el vértice A del triángulo las perpendiculares AF y AG a las exteriores y AE y AD a las interiores, demuéstrese que si unimos F con G, la recta resultante pasará por los puntos E y D.
Bruño (1963): Geometría. Curso superior. Solucionario. Editorial Bruño. Madrid.
Solución de F. Damián Aranda Ballesteros
| |
|
| Como quiera que por construcción, AF y AD son
perpendiculares a BF y BD, respectivamente, y por otro lado, BF y BD
son perpendiculares entre sí, por tratarse de las dos bisectrices del
mismo ángulo en B, una exterior y la otra interior, resultará que la
figura ADBF será un rectángulo con una de sus diagonales, el lado c
= AB. Por ello, J, punto medio del lado AB, será el centro de la circunferencia
circunscrita al rectángulo ADBF y así el ángulo <AFD será igual al
ángulo <ABD =<IBC=<1/2×B. Así tenemos que la recta FD, diagonal del rectángulo ADBF,
será paralela al lado BC por J, punto medio del lado AB. En resumen,
la recta DF será la paralela media al lado BC en el triángulo ABC inicial.
|
|