Problema 118.- Cuatro puntos alineados.

 137.- Si en un triángulo cualesquiera ABC se trazan las bisectrices exteriores e interiores de los  ángulos B y C,  y luego se bajan desde el vértice A del triángulo las perpendiculares AF y AG a las exteriores y AE y AD a las interiores, demuéstrese que si unimos F con G, la recta resultante pasará por los puntos E y D.

Bruño (1963): Geometría. Curso superior. Solucionario. Editorial Bruño. Madrid. (pág 64)

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León de Salamanca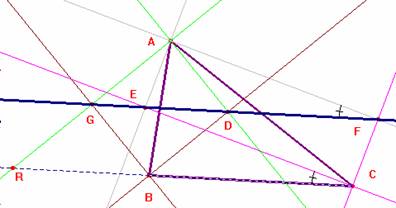.- Por la construcción quedan determinados los paralelogramos (rectángulos) AFCE  y ADBG. En efecto: AF es paralela a EC por ser ambos perpendiculares a la bisectriz exterior de C. AE es paralela a FC por ser ambas perpendiculares a la bisectriz interior de C. El mismo argumento respecto a las bisectrices de B demuestra que también es un paralelogramo rectángulo ADBG.

El segmento FE es paralelo a BC pues los ángulos EFA y ECA = BCE son iguales y AF y EC son paralelas. De igual modo resultan paralelas GD y BC ya que los ángulos ADG y GBA=GBR son iguales. Por las propiedades de los paralelogramos, GD corta a AB en su punto medio, y EF  a AC en su punto medio; resulta que los puntos E y D , F y G, son puntos de una misma recta: la paralela media, y por tanto yacen todos sobre ella. c.q.d.