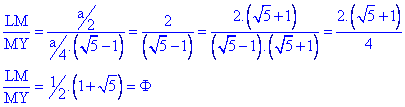Problema 119

Sea ABC un triángulo equilátero. Tracemos la circunferencia circunscrita. Sean L y M los puntos medios de AB y AC.
La recta LM corta a la circunferencia en X e Y.
Demostrar que LM/MY= Número de oro.

Rigby, J. F.(1988): Equilateral triangles and the golden ratio. Mathematical Gazette (Marzo 1988) pp. 27-30

Solución de F. Damián Aranda Ballesteros

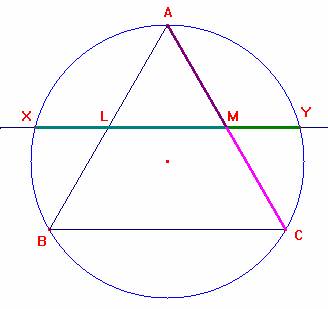Sea ABC el triángulo equilátero de lado a. Nombraremos a los segmentos siguientes por sus respectivas longitudes de forma que:

MY = XL = x

AM = MC = a/2

Consideramos el valor de la potencia del punto M respecto a la circunferencia circunscrita al triángulo dado.
Así, podemos expresar la siguiente identidad:
MY×MX = MA×MC ,es decir,
x×(x+a/2)=(a/2)²;
x²+a/2×x-a²/4=0;

En definitiva: