Propuesto por el profesor Juan Bosco Romero Márquez, colaborador de la Universidad de Valladolid

Problema 119

Sea ABC un triángulo equilátero.

Tracemos la circunferencia circunscrita.

Sean L y M los puntos medios de AB y AC.

La recta LM corta a la circunferencia en X e Y.

Demostrar que LM/MY= número de oro

Rigby, J. F.(1988): Equilateral triangles and the golden ratio. Mathematical Gazette (marzo 1988) pp. 27-30

Solución de Maite Peña Alcaraz, alumna del Colegio Porta Celi (Sevilla)

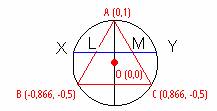
Si vemos; la recta LM será y=1/4; ya que pasará por el punto medio de la altura del triángulo. La circunferencia será x²+y²=1; y por tanto Y tendrán componente x=15^(1/2)/4.

Es evidente que al ser M el punto medio de AC su componente x será la mitad de C; luego M=(3^(1/2)/4, 0,25), L=(-3^(1/2)/4, 0,25) e Y=(15^(1/2)/4, 0,25)

y por tanto LM/MY=[3^(1/2)/2]/[(15^(1/2)/4-3^(1/2)/4)= 2/(5^(1/2)-1) que es igual al número de oro.