Problema 119
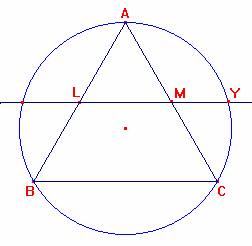
Sea ABC un triángulo equilátero.
Tracemos la circunferencia circunscrita.
Sean L y M los puntos medios de AB y AC.
La recta LM corta a la circunferencia en X e Y.
Demostrar que LM/MY= número de oro.
Solución del profesor Nicolás Rosillo. IES Máximo Laguna, Santa Cruz de Mudela, Ciudad Real (1 de noviembre de 2003)
La configuración del problema puede reducirse a esta:
|
|
|
En su magnífico libro “La experiencia de descubrir en geometría” (Ed. Nivola), Miguel de Guzmán da el siguiente resultado para el programa de cómputo simbólico DERIVE:
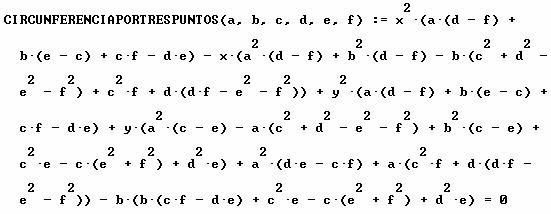
que aplicada a nuestro problema devuelve el siguiente resultado:
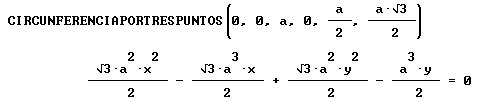
Resolviendo el sistema formado por la circunferencia obtenida y la recta LM se obtienen las coordenadas de los puntos X e Y.
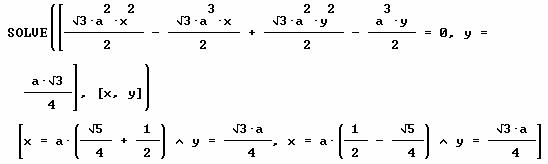
El punto Y tiene de coordenadas las de la primera solución obtenida. Se restan de las coordenadas de M para obtener la longitud del segmento MY
![]()
devolviendo el programa
![]()
y pidiendo el calculo del cociente LM/MY
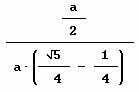
se obtiene el resultado deseado.
![]()
Nicolás Rosillo.