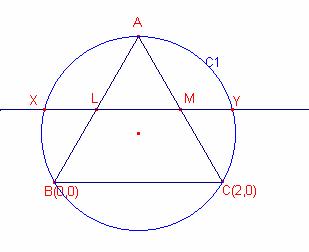
Siga el triangle equilàter .

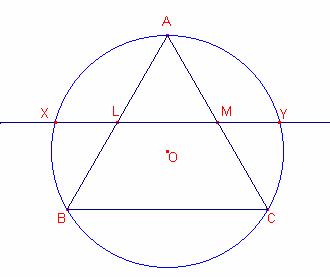
Siguen L, M els punts migs dels segments AB, AC, respectivament.

Siga C1 la circumferència circumscrita al triangle .

La recta que passa pels punts L, M talla la circumferència C1 en els punts X, Y.

Proveu que

Solución de Ricard Peiró

Solució: (Amb coordenades cartesinanes).

Considerem El triangle , tal que B(0,0), C(2,0).

Per ser el triangle equilàter

Les coordenades dels punts L, M són:

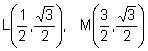
Siga C1 la circumferència circumscrita al triangle  de centre O i radi R

El centre O té coordenades

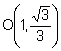
El radi de la circumferència circumscrita C1 és:

L’equació de la circumferència C1 és:

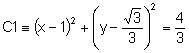
L’equació de la recta r que passa pels punts L, M és:

Les interseccions de la circumferència C1 i la recta r són:

,

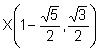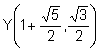
Aleshores:

Demostració trigonomètrica:

Considerem el triangle  de costat

Aplicant el teorema de Pitàgores al triangle

Aleshores

Considerem el triangle

Per la propietat del baricentre del triangle

L’angle

Considerem el triangle

Aplicant el teorema del cosinus al triangle

Simplificant:

Aleshores,