Problema 119

Sea el triángulo equilátero .

Sean L, M los puntos medios de los segmentos AB, AC, respectivamente.

Sea C1 la circunferencia circunscrita al triángulo .

La recta que pasa por los puntos L, M corta a la circunferencia C1 en los puntos X, Y.

Demostrar que  

Solución de Ricard Peiró y Estruch:

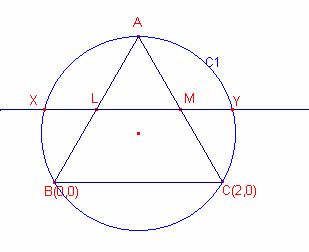
Solución: (en coordenadas cartesinanas).

Consideremos el triángolo , tal que B(0,0), C(2,0).

Por ser el triangulo equilátero

Las coordenadas de los puntos L, M son:

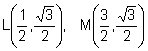
Sea C1 la circunferencia circunscrita al triángulo  de centro O y radio R

El centro O tiene de coordenadas

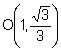
El radio de la circunferencia circunscrita C1 es:

La ecuación de la circunferencia C1 es:

La ecuación de la recta r que pasa por los puntos L, M es:

Las intersecciones de la circunferencia C1 y la recta r son:

,

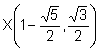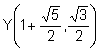
Entonces:

Demostració trigonomètrica:

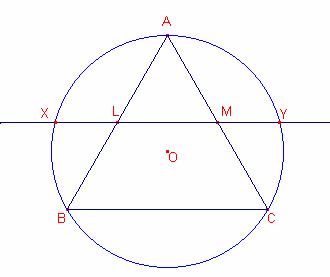
Consideremos el triángulo  de lado

Aplicando el teorema de Pitàgoras al triángulo

Entonces

Consideremos el triángulo

Por la propiedad del baricentro del triángulo

El ángulo  

Consideremos el triángulo

Aplicando el teorema del coseno al triángulo

Simplificando:

Entonces,