Problema 119.- Sea ABC un triángulo equilátero. Tracemos la circunferencia circunscrita.
Sean L y M los puntos medios de AB y AC. La recta LM corta a la circunferencia en X e Y.
Demostrar que LM/MY= número de oro.
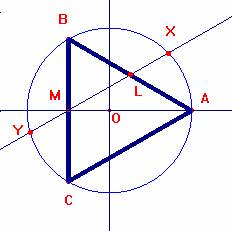Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León de Salamanca.- Supongamos que los vértices del triángulo equilátero ABC son los afijos de las soluciones complejas de la ecuación z3 = 1. (Tomamos el lado del triángulo equilátero igual a la unidad). Son pues, los afijos de los números complejos z1 = 1, z2 = 
; z3 = 
respectivamente. La suma de los tres es igual a cero, siendo complejos conjugados los dos últimos y su producto igual a la unidad. A su vez, los puntos L y M son los afijos de los números complejos zL = ½( z1 + z2); zM = ½(z2 + z3); LM viene representado por el número complejo zLM = ½(z3 – z1). Los vectores LM y MY tienen el mismo sentido, si expresamos LM = aMY, por estar sobre la misma recta, el escalar a ha de ser un número real positivo.
El punto Y es el afijo del número complejo zY = zM + zMY = ½(z2 + z3) +1/a· zLM = ½(z2 + z3) +1/a ·½(z3 – z1). Multiplicando por 2a, tendremos 2a·zY =a( z2 + z3)+ z3 – z1 = –a + z3 – 1. Para que Y esté sobre la circunferencia unidad, el módulo de su vector representativo zY, ha de ser igual a 1, o de forma equivalente, z3 –(1+a) ha de tener módulo 2a.
Para calcular este módulo multiplicamos por su conjugado, el número, z2 –(1+a) obteniendo así el cuadrado del mismo.
4a2 = [z3–(1+a)][z2–(1+a)]=(1+a)2—( z2 + z3)(1+a) + z2 z3 .
Sustituyendo la suma y el producto de los complejos que aparecen en la expresión anterior se tiene 4a2 = (1+a)2 + (1+a) + 1. Desarrollando y trasponiendo términos resulta
3a2 -- 3a - 3 = 0 o bien a2 - a - 1 = 0, que es la ecuación que verifica el número de oro. Con esto queda demostrado que a = 
es el número de oro.