Problema 120.- Construir un triangulo conociendo las 3 bisectrices.

(Comunicación personal por e-mail de fpastre@adinet.com.uy.

Solución parcial del profesor Saturnino Campo Ruiz, del IES Fray Luis de León, de Salamanca.-  

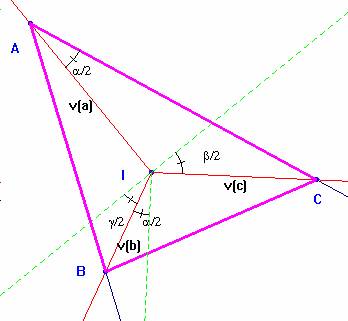
Entendemos que dar las tres bisectrices es dar las tres rectas en posición v_a, v_b y v_c, concurrentes en el incentro I. Para que el problema quede determinado habremos de dar un punto A  sobre la  bisectriz v_a. En otro caso habrá infinidad de soluciones.

Supongamos el problema resuelto. Un sencillo cálculo nos permite obtener el valor de los ángulos formados desde el incentro: BIC=90+a/2;               BIA = 90 + g/2;   AIC = 90+ b/2.  Restando a estos ángulos un recto, se obtienen los ángulos mitad de los del triángulo buscado.

Para construir el triángulo basta con trazar desde A semirrectas que formen con la bisectriz AI ángulos iguales a a/2 como se ve en la figura. Estas semirrectas cortan a v_c en el vértice C y a v_b en el vértice B, quedando resuelto el problema.