Problema 122
Construir un triángulo isósceles conocido el lado igual y el radio de la circunferencia inscrita.
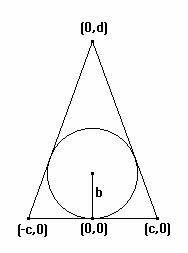
La configuración puede reducirse a esta:
|
|
Asignamos el valor a a la longitud del lado igual y b al radio de la circunferencia inscrita. Los puntos del triángulo deben cumplir Por otro lado, la ecuación de la recta que pasa por (0,d) y (c,0) es
Y la ecuación de la circunferencia inscrita es
|
Si la circunferencia es inscrita al triángulo, el sistema formado por la recta y la circunferencia ha de tener solución única.
Con DERIVE 5 se realiza la resolución del sistema
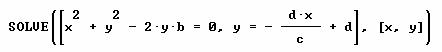
obteniendo

Para que las dos soluciones sean iguales
![]()
Con lo cual, las coordenadas del triángulo deseado se obtienen resolviendo el sistema formado por
![]() y
y ![]()
Desgraciadamente, el aspecto de las soluciones es espantoso y nada fácilmente reproducible, por lo que sólo se muestran soluciones obtenidas con datos numéricos. Así, para a=8 y b =2

Las parejas 3 y 4 (ambas con d negativa) no sirven. Las otras cuatro dan coordenadas de c y d correctas.