Propuesta de Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid.
Problema 123

Sea ABC un triángulo escaleno de lados conocidos, a=BC, b=AC y c=AB.
Tomando como referencia por ejemplo, el vértice A, -la misma construcción se harían por los vértices B y C-, se hace la siguiente construcción:
Con centro en los vértices B y C, respectivamente, trazamos circunferencias que pasan por A, y cortan en los puntos M y N, respectivamente sobre la recta BC, siendo M el punto más cercano a C, y N el más cercano a B.
Por M dibujamos la paralela MD al lado AB, y de igual longitud; lo mismo por el punto N dibujamos la paralela NE al lado AC y de igual longitud.
De esta forma hemos obtenido los paralelogramos, AMDB, MD=AB , y, ANEC, NE=AC.
Probar:
a) Los puntos F(A) = intersección de MD y EN, A´= intersección de CE con BD, y A, son colineales siendo la recta que los contiene la bisectriz interior del ángulo, A.
b) ¿ Qué relación geométrica existe entre los triángulos A' B'C' y F(A), F(B) F(C), con respecto al triángulo ABC ?

Romero Márquez, J.B. (2003): Comunicación personal.

Solución de Daminán Aranda Ballesteros

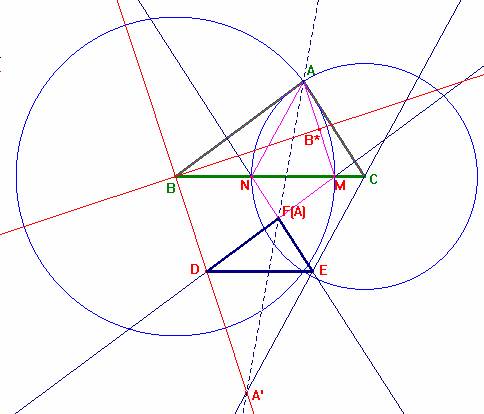
Si consideramos el triángulos isósceles ABM; (BA=BM) y sobre la base AM, su punto medio B*, entonces la recta BB* será la bisectriz del ángulo <A del triángulo ABC y, como esta recta es perpendicular al lado AM, lo será también a la recta BD. Por tanto, BD será la bisectriz exterior del ángulo <A en el triángulo inicial ABC. Del mismo modo, se prueba que el punto A’ pertenecerá también a la bisectriz exterior del ángulo C; luego el punto A' es el exincentro correspondiente al ángulo A del triángulo ABC. De este modo, A’ pertenecerá también a la bisectriz interna del triángulo ABC correspondiente al ángulo <A.

Veamos ahora cómo el triángulo F(A)DE es semejante al inicial ABC. Para ello, tenemos que el ángulo en F(A) es igual al ángulo A y, como ahora veremos, la razón de sus lados es igual a b/c.

Calculamos la longitud del lado F(A)D y F(A)E.

F(A)E = b - b/a∙2(s-a)

F(A)D = c - c/a∙2(s-a), donde 2s = a + b + c.

Por tanto,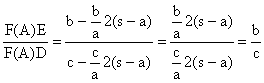

Luego, en efecto, ambos triángulos son semejantes. Como los puntos homólogos B y D, por un lado y C y E, por otro, están alineados con el punto A’, también lo estarán A y F(A) con A’, c.q.d.

b) ¿ Qué relación geométrica existe entre los triángulos A' B'C' y F(A), F(B) F(C), con respecto al triángulo ABC ?

*El triángulo A’B’C’ es el formado por los exincentros del triángulo ABC. Por tanto, el triángulo ABC es el triángulo órtico del A’B’C’.

*Por otro lado, el punto F(A) es el transformado de A por la homotecia de centro el punto A’ y razón . De igual manera, el punto F(B) es el transformado de B por la homotecia de centro el punto B’ y razón y el punto F(C) es el transformado de C por la homotecia de centro el punto C’ y razón .