Propuesta del profesor Ricard Peiró, del IES 1 de
Cheste
Problema
124
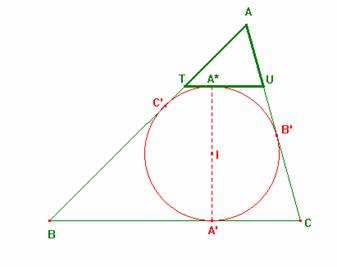
Sea el triángulo ABC y su
circunferencia inscrita C de radio r. Sean las rectas tangentes a la
circunferencia C paralelas a los lados del triángulo, que determinan con los
vértices los triángulos PQC, RSB, TUA.
En cada triángulo, construimos la circunferencia inscrita de radios r1,
r2, r3, respectivamente.
Entonces: r = r1 + r2 + r3
Peiró i Estruch, R. (2003): Comunicación personal
Solución de F. Damián Aranda Ballesteros
Por la propia construcción hecha, se tiene que el triángulo ATU y el dado inicialmente ABC son semejantes.
Si llamamos A* al punto de contacto de la circunferencia inscrita C con el triángulo ATU, se tendrán las siguientes igualdades entre segmentos:
TA*=TC' = x1
UA*=UB' = x2
AC' = AB' =
s-a, donde:
2s = a + b + c.
Así entonces, podemos expresar los lados del triángulo ATU del modo siguiente:
AT= s-a-x1
AU= s-a-x2
TU= x1 + x2
Por tanto, su área vendrá dada por la
expresión:
S[ATU]= 1/2×[(s-a-x1) + (s-a-x2) + (x1
+ x2) ]×r3 = (s-a)×r3
Por otro lado, el área del triángulo ABC será: S[ABC]= s×r
Así podemos expresar las razones de las áreas de ambos triángulos semejantes como:
.
Por otro lado, esta razón será igual al
cuadrado de la razón de semejanza entre ambos triángulos. Podemos relacionarlas
en esta igualdad:
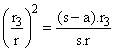; Despejando
r3, obtenemos que: 
.
Actuando de igual manera con los triángulos PQC y RSB,
obtendríamos las expresiones de r1 y r2, respectivamente: 
Sumando finalmente:
