Sea el triángulo 
y la circunferencia
inscrita C de radio r.
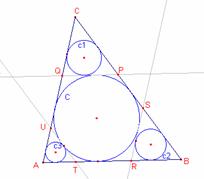Sean las rectas tangentes
a la circunferencia C paralelas a los lados
del triángulo, que determinan con los vértices los triángulo 
.
En cada triángulo, dibujamos la circunferencia inscrita de radios 
, respectivamente
.
Entonces:
Demostración de Ricard Peiró i Estruch:
El radio de la circunferencia inscrita al triángulo es:
donde
p es el semiperímetro del triángulo
Sean 
la altura
del triángulo referida al lado a del triángulo
La altura (aplicando la fórmula d’Heró) mide:
los triángulos ,
son semejantes
Sea 
la altura
del triángulo referida
al lado TU.
Entonces:
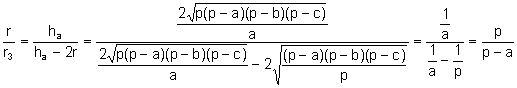
Análogamente:
los triángulos ,
son semejantes,
entonces:
los triángulos ,
son semejantes,
entonces:
Por tanto: 
,
,
Entonces:
