Problema 125
Sea P un punto del arco menor AB de la circunferencia circunscrita del triángulo equilátero ABC. Se tiene que, CP = AP + BP
Yiu P. (1998):"Euclidean Geometry" 1998. p.150

Solución de F. Damián Aranda Ballesteros.

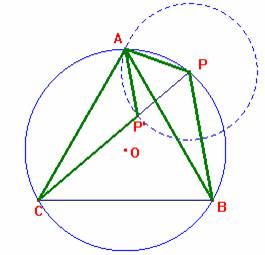El triángulo APP' es equilátero ya que el ángulo en P es igual al ángulo inscrito en la circunferencia <ABC= 60º y, por otra parte
PP' = PA, por la construcción hecha en la figura adjunta.

De este modo, veamos ahora cómo los triángulos AP'C y APB son congruentes. Este hecho es cierto sin más que probar que tienen dos ángulos iguales y uno de los lados homólogos iguales entre sí.
Para ello, tenemos que:
<APB = 120º = <AP'C; y que <ABP = <ACP' y así el tercer ángulo <CAP' = <BAP.
Como AP=AP' (también AC = AB) entonces se tendrá que: CP' = BP, pero como CP' = CP - AP.

En definitiva, BP = CP - AP, c.q.d.