----------------------

Propuesta del profesor Ricard Peiró, del IES 1 de Cheste

Problema 125

Sea P un punto del arco menor AB de la circunferencia circunscrita del triángulo equilátero ABC.

Se tiene que, CP=AP+BP

Yiu P. (1998):"Euclidean Geometry" 1998. p.150

Solución de Maite Peña Alcaraz:

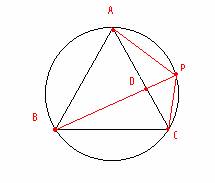
Siendo a el lado del triángulo equilátero ABC, y sabiendo que AD+AC=a

1.- Por el teorema del coseno,

BD²=CD²+a²-2aCDcos60º=CD²+a²-aCD

BD²=AD²+A²-2aADcos60º=AD²+a²-aAD luego

2BD²=CD²+AD²+2a²-a(CD+AD)=CD²+AD²+a²

2.- BAD y CDP son semejantes, así como BDC y ADP ya que existe una propiedad que dice que en una circunferencia circunscrita a un triángulo, coinciden la bisectriz de un ángulo y la mediatriz del lado opuesto. La mediatriz de AC corta a la circunferencia en B y PB pasa por el vértice opuesto y por B luego es la bisectriz de el ángulo APC, que mide 120º por propiedades del arco capaz, luego DPC=DPA=60º y por tanto tienen los tres ángulos iguales.

3.- De aquí que

BD/CD=a/PC=DA/PD

BD/AD=a/PA=CD/PD,

De dónde se podrían sustituir:

PD=DACD/BD

PA=aAD/BD

PC=aCD/BD

4.- Sustituyendo ahora en PB=PA+PC; BP+PD=PA+PC; BD+DACD/BD=aAD/BD+ aCD/BD; 2BD²+2DACD=2a(AD+CD)=2a²

y por último sustituyendo 2BD² se obtiene,

(CD+AD)²=a² lo que es evidente luego la igualdad es cierta.

------------------------------------------------------